Uncertainty Quantification by MLMC and Local Time-stepping For Wave Propagation

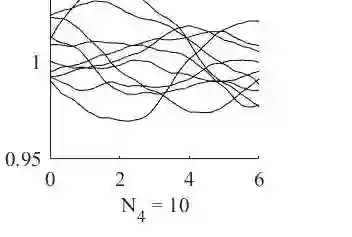
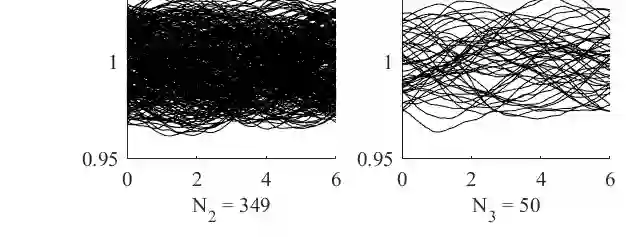
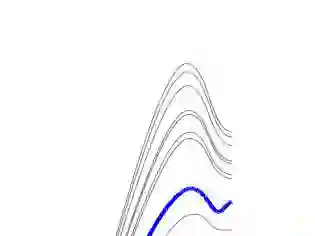
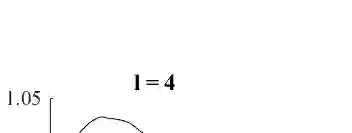Because of their robustness, efficiency and non-intrusiveness, Monte Carlo methods are probably the most popular approach in uncertainty quantification to computing expected values of quantities of interest (QoIs). Multilevel Monte Carlo (MLMC) methods significantly reduce the computational cost by distributing the sampling across a hierarchy of discretizations and allocating most samples to the coarser grids. For time dependent problems, spatial coarsening typically entails an increased time-step. Geometric constraints, however, may impede uniform coarsening thereby forcing some elements to remain small across all levels. If explicit time-stepping is used, the time-step will then be dictated by the smallest element on each level for numerical stability. Hence, the increasingly stringent CFL condition on the time-step on coarser levels significantly reduces the advantages of the multilevel approach. By adapting the time-step to the locally refined elements on each level, local time-stepping (LTS) methods permit to restore the efficiency of MLMC methods even in the presence of complex geometry without sacrificing the explicitness and inherent parallelism.