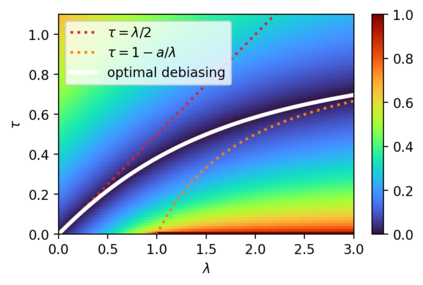
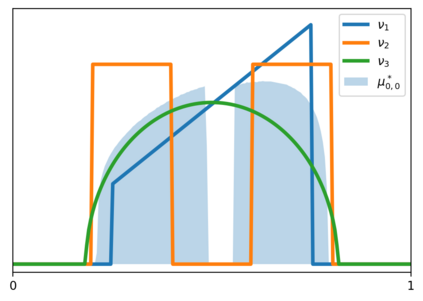
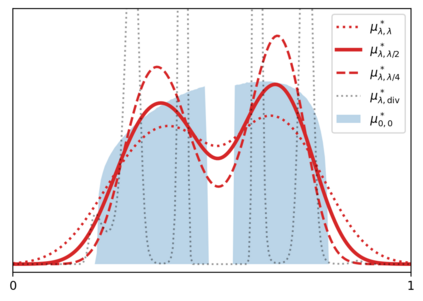
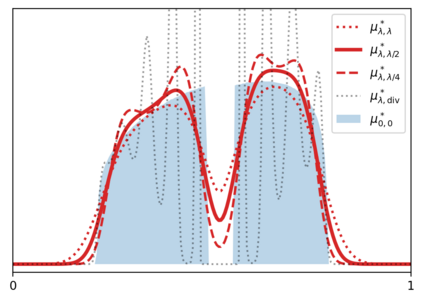
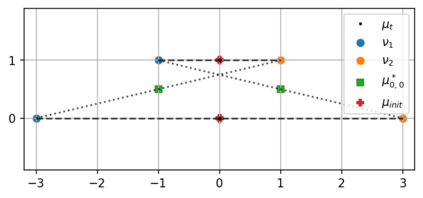
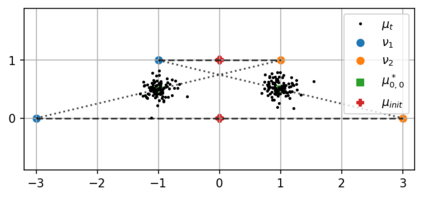
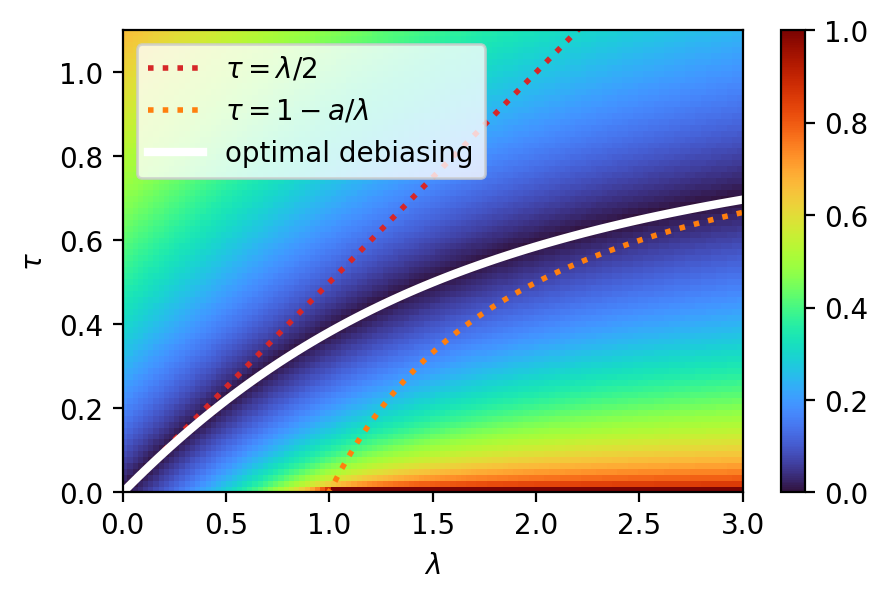
We study a general formulation of regularized Wasserstein barycenters that enjoys favorable regularity, approximation, stability and (grid-free) optimization properties. This barycenter is defined as the unique probability measure that minimizes the sum of entropic optimal transport (EOT) costs with respect to a family of given probability measures, plus an entropy term. We denote it $(\lambda,\tau)$-barycenter, where $\lambda$ is the inner regularization strength and $\tau$ the outer one. This formulation recovers several previously proposed EOT barycenters for various choices of $\lambda,\tau \geq 0$ and generalizes them. First, in spite of -- and in fact owing to -- being \emph{doubly} regularized, we show that our formulation is debiased for $\tau=\lambda/2$: the suboptimality in the (unregularized) Wasserstein barycenter objective is, for smooth densities, of the order of the strength $\lambda^2$ of entropic regularization, instead of $\max\{\lambda,\tau\}$ in general. We discuss this phenomenon for isotropic Gaussians where all $(\lambda,\tau)$-barycenters have closed form. Second, we show that for $\lambda,\tau>0$, this barycenter has a smooth density and is strongly stable under perturbation of the marginals. In particular, it can be estimated efficiently: given $n$ samples from each of the probability measures, it converges in relative entropy to the population barycenter at a rate $n^{-1/2}$. And finally, this formulation lends itself naturally to a grid-free optimization algorithm: we propose a simple \emph{noisy particle gradient descent} which, in the mean-field limit, converges globally at an exponential rate to the barycenter.
翻译:我们研究了一种正则化 Wasserstein barycenters 的通用公式,该公式具有有利的正则化、逼近、稳定性和(无网格)优化特性。该 barycenter 被定义为唯一的概率测度,它最小化了与一组给定概率测度相关的熵最优传输(EOT)成本之和,再加上熵项。我们将其表示为 $(\lambda,\tau)$-barycenter,其中 $\lambda$ 是内部正则化强度,$\tau$ 是外部正则化强度。这个公式恢复了以前提出的各种选择 $\lambda,\tau \geq 0$ 的 EOT barycenters,并将它们推广了。首先,我们证明了尽管它被 \emph{doubly} 正则化,但它对于 $\tau=\lambda/2$ 是未偏的:对于光滑密度,无(非正则化)Wasserstein barycenter 目标的次优性是熵正则化强度 $\lambda^2$ 的阶,而不是通常的 $\max\{\lambda,\tau\}$。我们讨论了各向同性高斯分布下的这种现象,其中所有 $(\lambda,\tau)$-barycenters 都具有封闭形式。其次,我们证明了对于 $\lambda,\tau>0$,这个 barycenter 具有平滑的密度,并且在边缘扰动下具有强稳定性。特别地,它可以被有效地估计:给定每个概率测量的 $n$ 个样本,它以速度 $n^{-1/2}$ 收敛于集合 barycenter 的相对熵率。最后,该公式自然地适用于基于网格的优化算法:我们提出了一个简单的 \emph{noisy particle gradient descent} 算法,在均场极限下,它全局指数速度收敛于 barycenter。