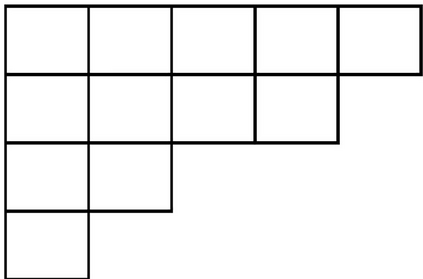
We propose and examine two optimal $(0,1)$-matrix completion problems with majorization ordered objectives. They elevate the seminal study by Gale and Ryser from feasibility to optimality in partial order programming (POP), referring to optimization with partially ordered objectives. We showcase their applications in electric vehicle charging, portfolio optimization, and secure data storage. Solving such integer POP (iPOP) problems is challenging because of the possible non-comparability among objective values and the integer requirements. Nevertheless, we prove the essential uniqueness of all optimal objective values and identify two particular ones for each of the two inherently symmetric iPOP problems. Furthermore, for every optimal objective value, we decompose the construction of an associated optimal~$(0,1)$-matrix into a series of sorting processes, respectively agreeing with the rule of thumb "peak shaving" or "valley filling." We show that the resulting algorithms have linear time complexities and verify their empirical efficiency via numerical simulations compared to the standard order-preserving method for POP.
翻译:我们提出并研究两大最佳目标完成问题。 他们将Gale 和 Ryser 的原始研究从可行性提升到局部排序方案(POP)中的最佳性, 指的是部分排序目标的优化。 我们展示其在电动车辆充电、组合优化和安全数据存储方面的应用。 解决此类整数持久性有机污染物( iPOP) 问题具有挑战性, 因为目标值和整数要求之间可能无法比较。 然而, 我们证明所有最佳目标值的基本独特性, 并为两个内在的对称 iPOP 问题中的每个问题确定两个特定问题。 此外, 对于每一个最佳目标值, 我们将相关的最佳 $~ ( 0. 1美元) 的构建分解成一系列分类过程, 分别同意拇指“ 峰底剃除” 或“ valley 填充” 规则 。 我们显示, 由此产生的算法具有线性的时间复杂性, 并通过数字模拟来验证其经验效率, 与持久性有机污染物的标准维持秩序方法相比较。