Dimension reduction and redundancy removal through successive Schmidt decompositions

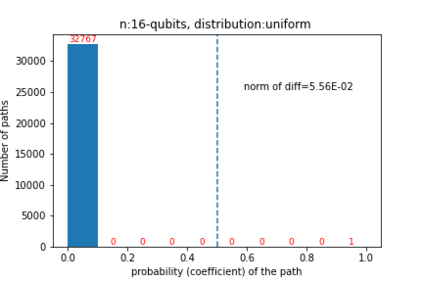
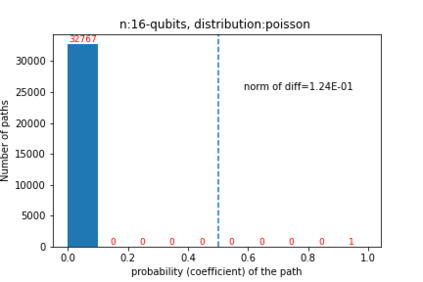
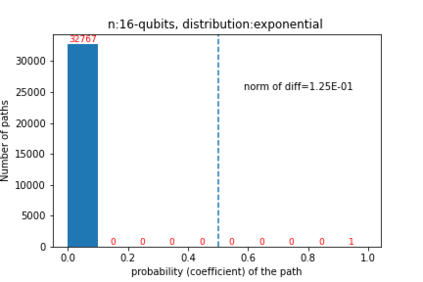
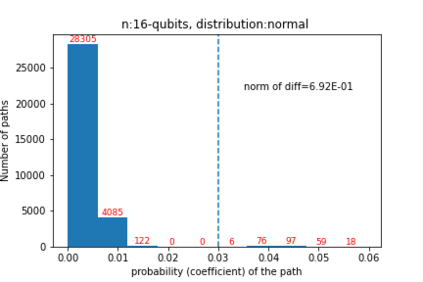
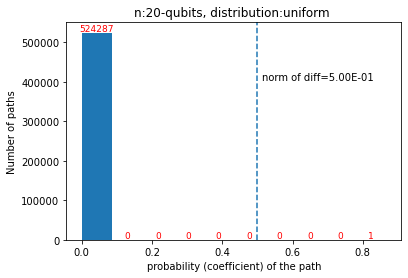
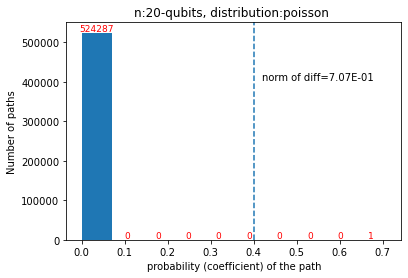
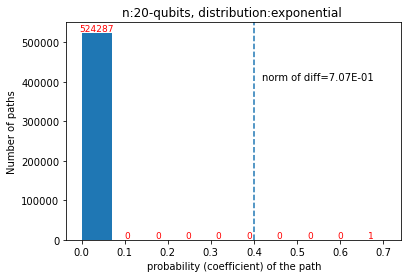
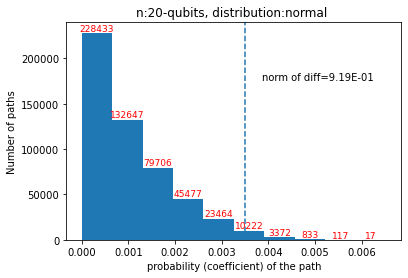
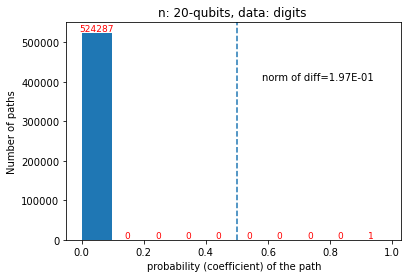
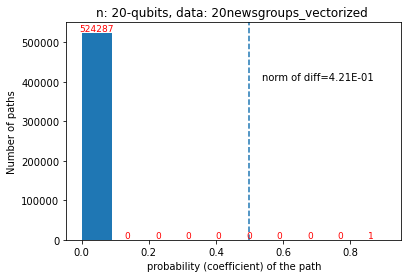
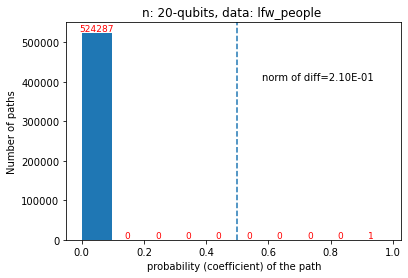
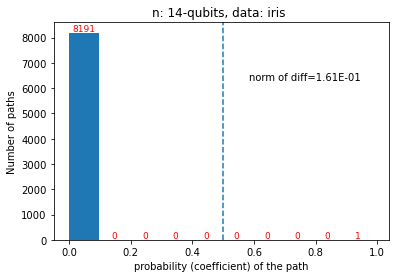
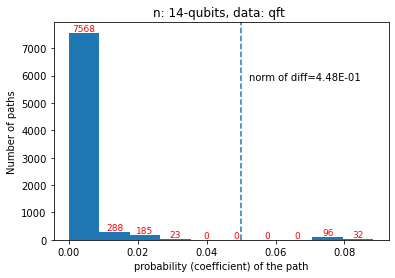
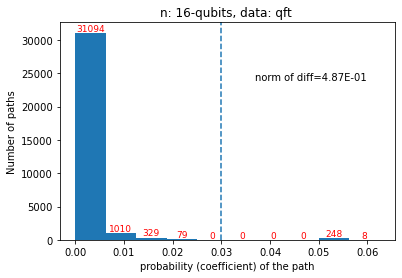
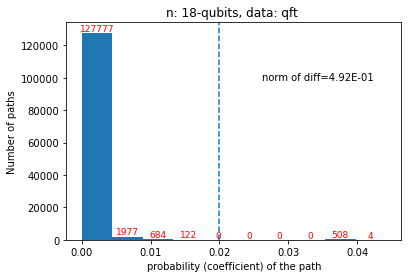
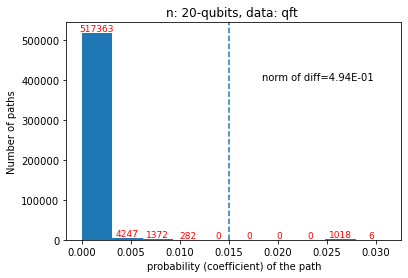
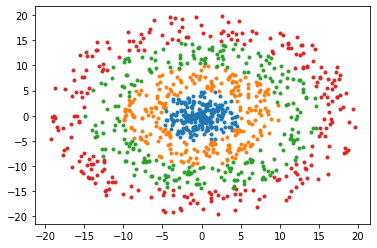
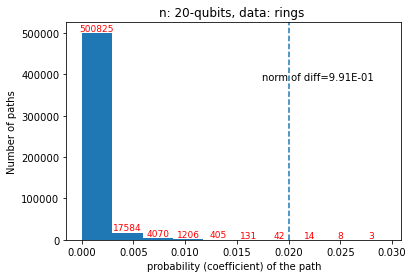
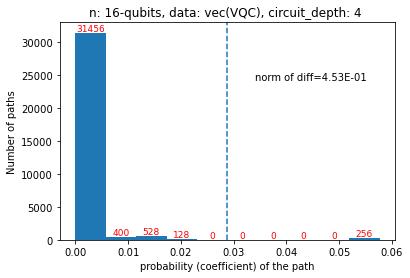
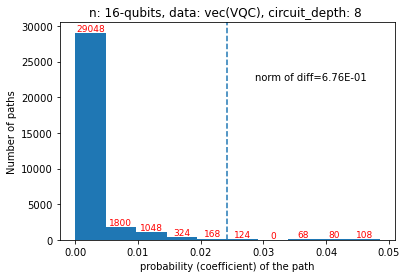
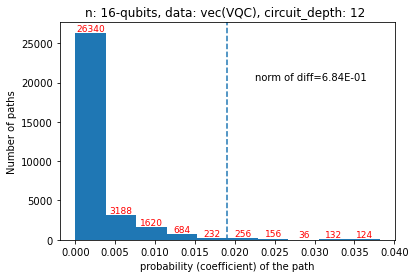
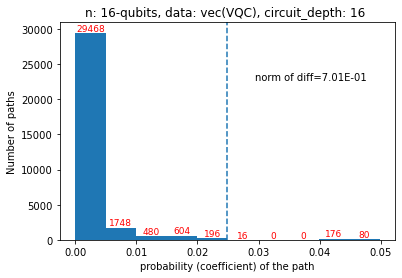
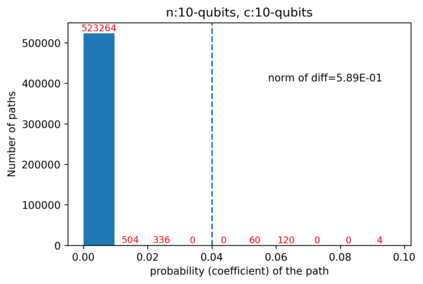
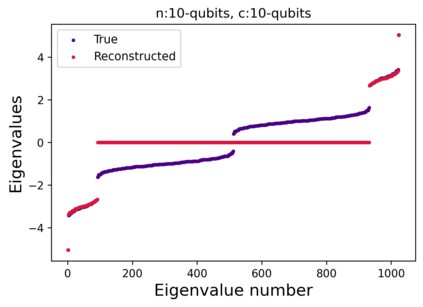
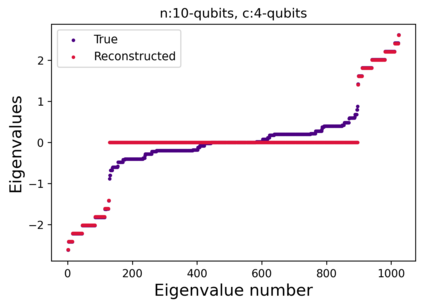
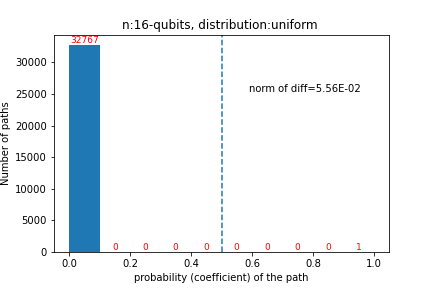
Quantum computers are believed to have the ability to process huge data sizes which can be seen in machine learning applications. In these applications, the data in general is classical. Therefore, to process them on a quantum computer, there is a need for efficient methods which can be used to map classical data on quantum states in a concise manner. On the other hand, to verify the results of quantum computers and study quantum algorithms, we need to be able to approximate quantum operations into forms that are easier to simulate on classical computers with some errors. Motivated by these needs, in this paper we study the approximation of matrices and vectors by using their tensor products obtained through successive Schmidt decompositions. We show that data with distributions such as uniform, Poisson, exponential, or similar to these distributions can be approximated by using only a few terms which can be easily mapped onto quantum circuits. The examples include random data with different distributions, the Gram matrices of iris flower, handwritten digits, 20newsgroup, and labeled faces in the wild. And similarly, some quantum operations such as quantum Fourier transform and variational quantum circuits with a small depth also may be approximated with a few terms that are easier to simulate on classical computers. Furthermore, we show how the method can be used to simplify quantum Hamiltonians: In particular, we show the application to randomly generated transverse field Ising model Hamiltonians. The reduced Hamiltonians can be mapped into quantum circuits easily and therefore can be simulated more efficiently.