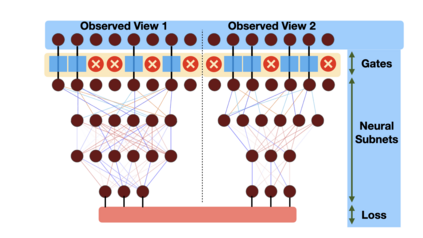
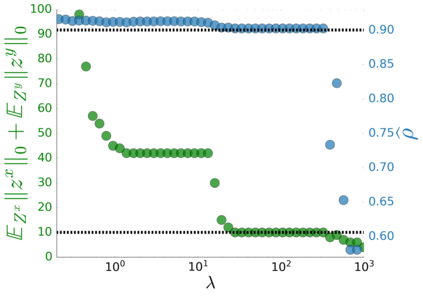
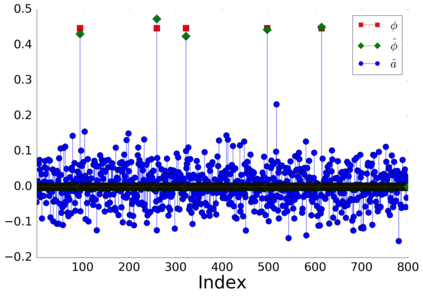
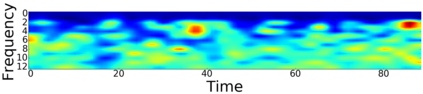
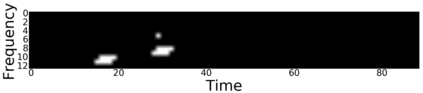
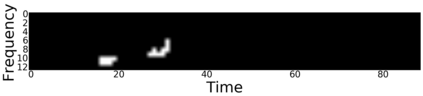
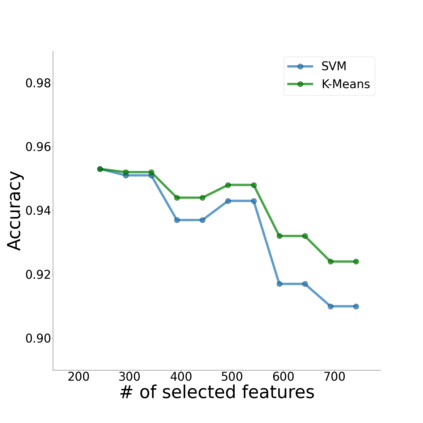
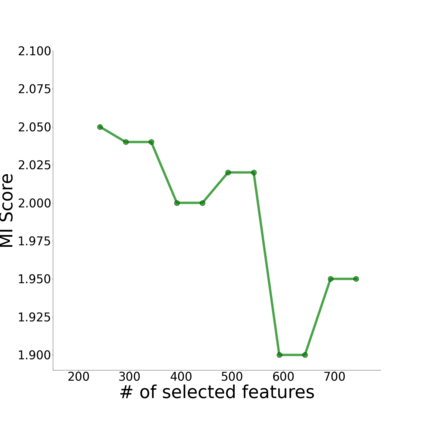
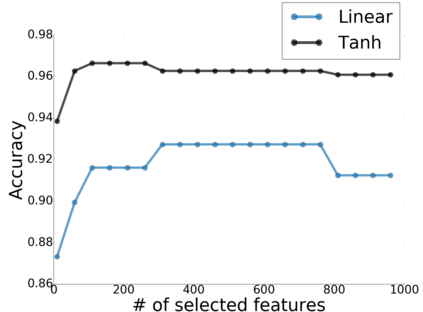
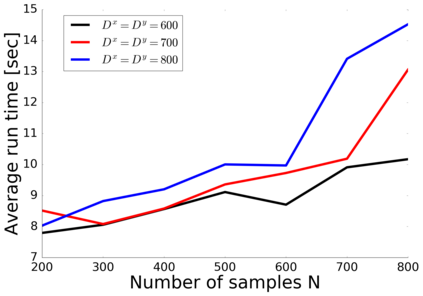
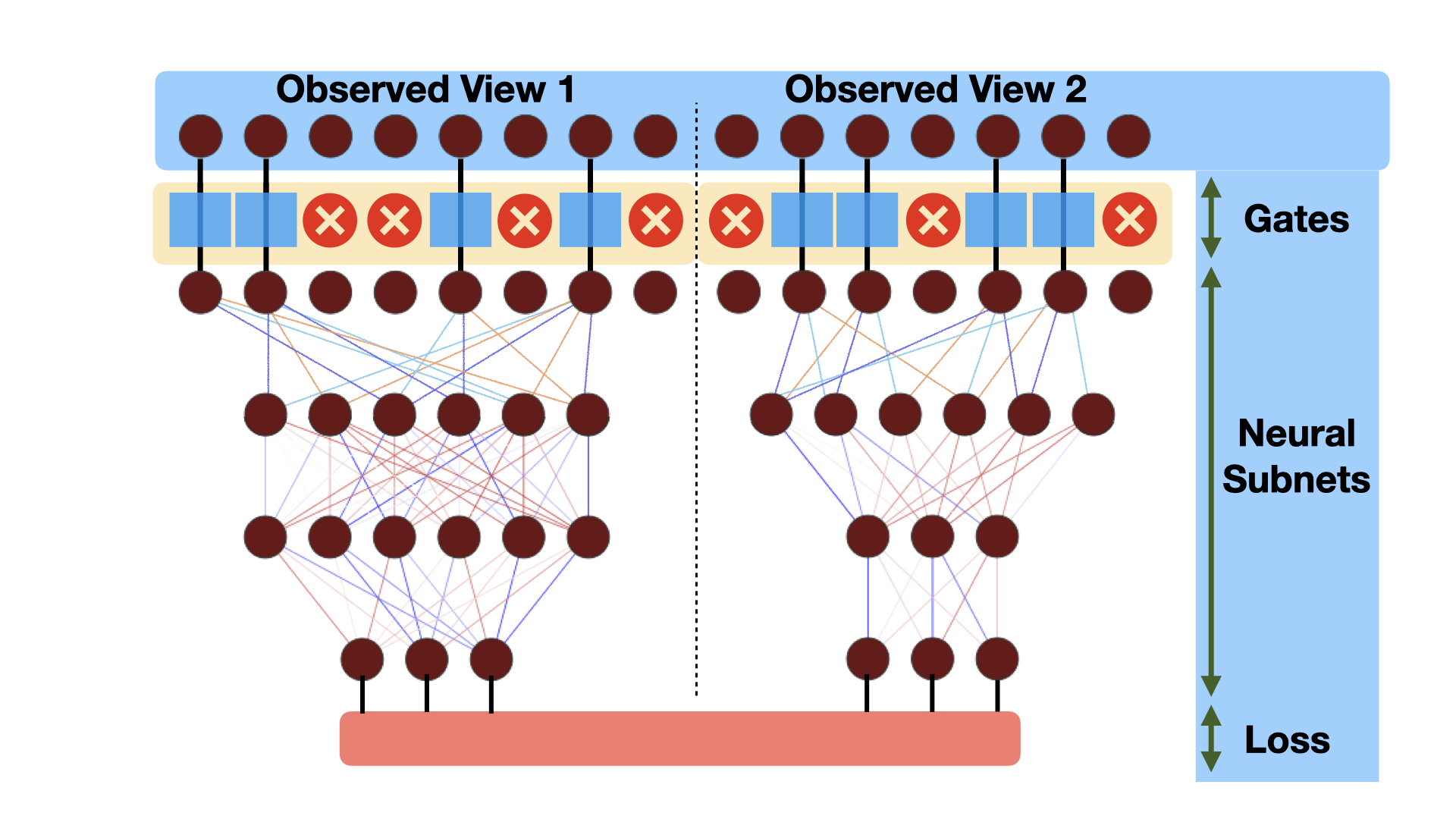
Canonical Correlation Analysis (CCA) models are powerful for studying the associations between two sets of variables. The canonically correlated representations, termed \textit{canonical variates} are widely used in unsupervised learning to analyze unlabeled multi-modal registered datasets. Despite their success, CCA models may break (or overfit) if the number of variables in either of the modalities exceeds the number of samples. Moreover, often a significant fraction of the variables measures modality-specific information, and thus removing them is beneficial for identifying the \textit{canonically correlated variates}. Here, we propose $\ell_0$-CCA, a method for learning correlated representations based on sparse subsets of variables from two observed modalities. Sparsity is obtained by multiplying the input variables by stochastic gates, whose parameters are learned together with the CCA weights via an $\ell_0$-regularized correlation loss. We further propose $\ell_0$-Deep CCA for solving the problem of non-linear sparse CCA by modeling the correlated representations using deep nets. We demonstrate the efficacy of the method using several synthetic and real examples. Most notably, by gating nuisance input variables, our approach improves the extracted representations compared to other linear, non-linear and sparse CCA-based models.
翻译:Canonic Connectrical Africa (CCA) 模型对于研究两组变量之间的关联作用很大。 被称为\ textit{canonical variates} 的 Canonical complates (CCA) 模型被广泛用于无监督的学习, 分析未贴标签的多式登记数据集。 尽管这些模型取得了成功, 但是如果两种模式中的变量数量都超过样本数量, 则Condical complicals Complication (CA) 模型可能会打破( 或过度使用) 。 此外, 变量计量模式特定信息中的一大部分往往有利于确定\ textit{cancontinual contric concolates 。 在这里, 我们提出 $\ ell_ 0 $- Deep CCA, 用于学习基于两种观察到的变量的稀少组别组别组别, 用于学习关联性表达方式的方法。 我们用最深网的模型, 和最不精确的模型, 展示了我们的方法, 改进了计算方法的效能。