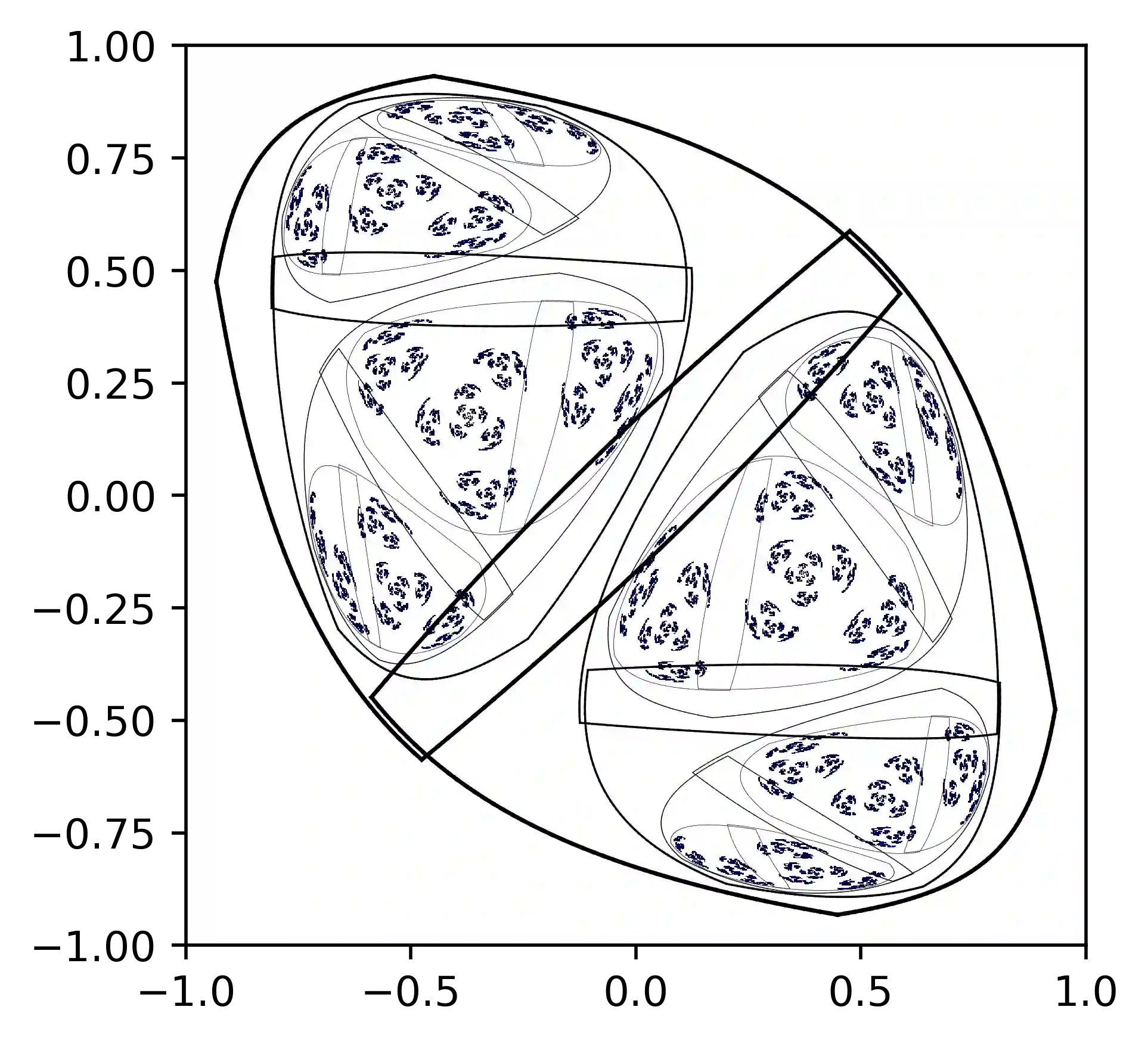
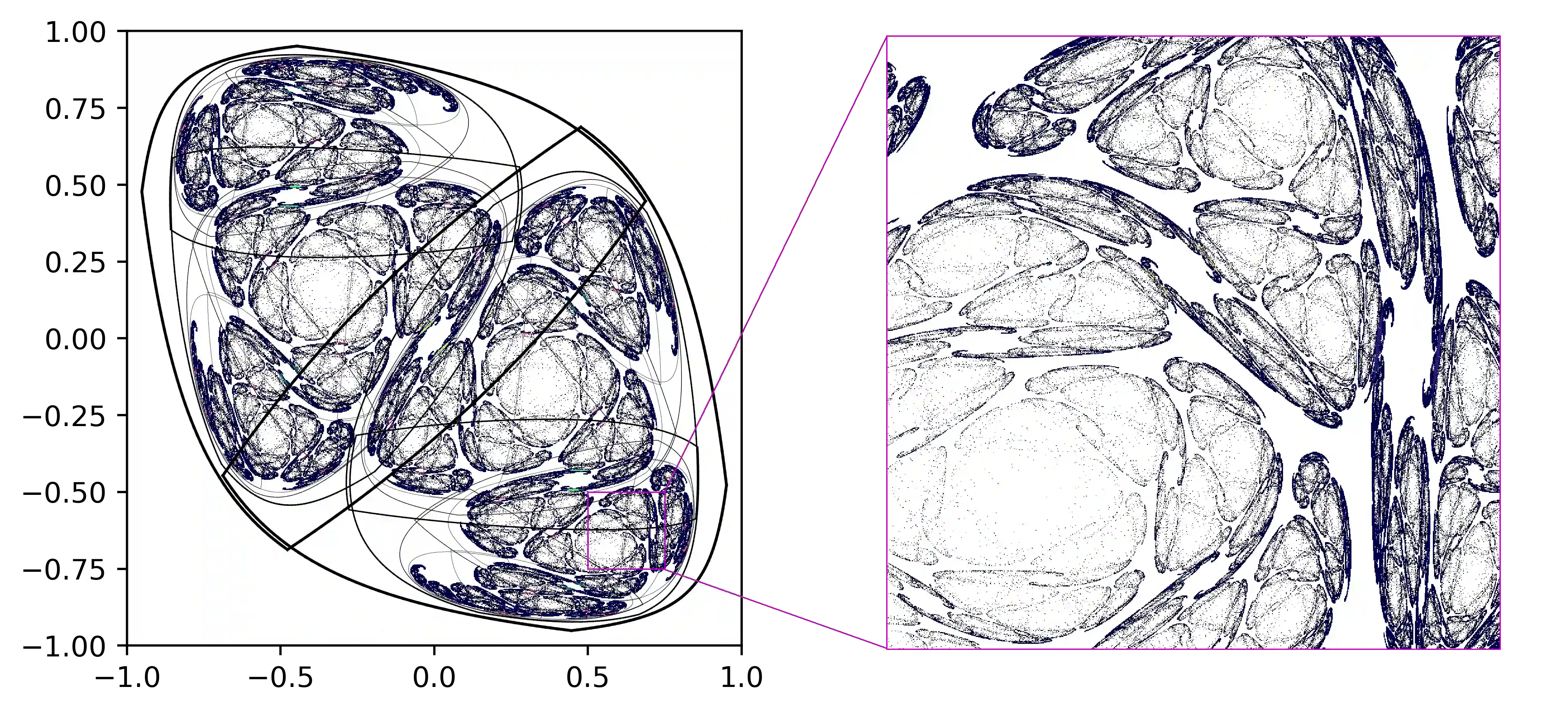
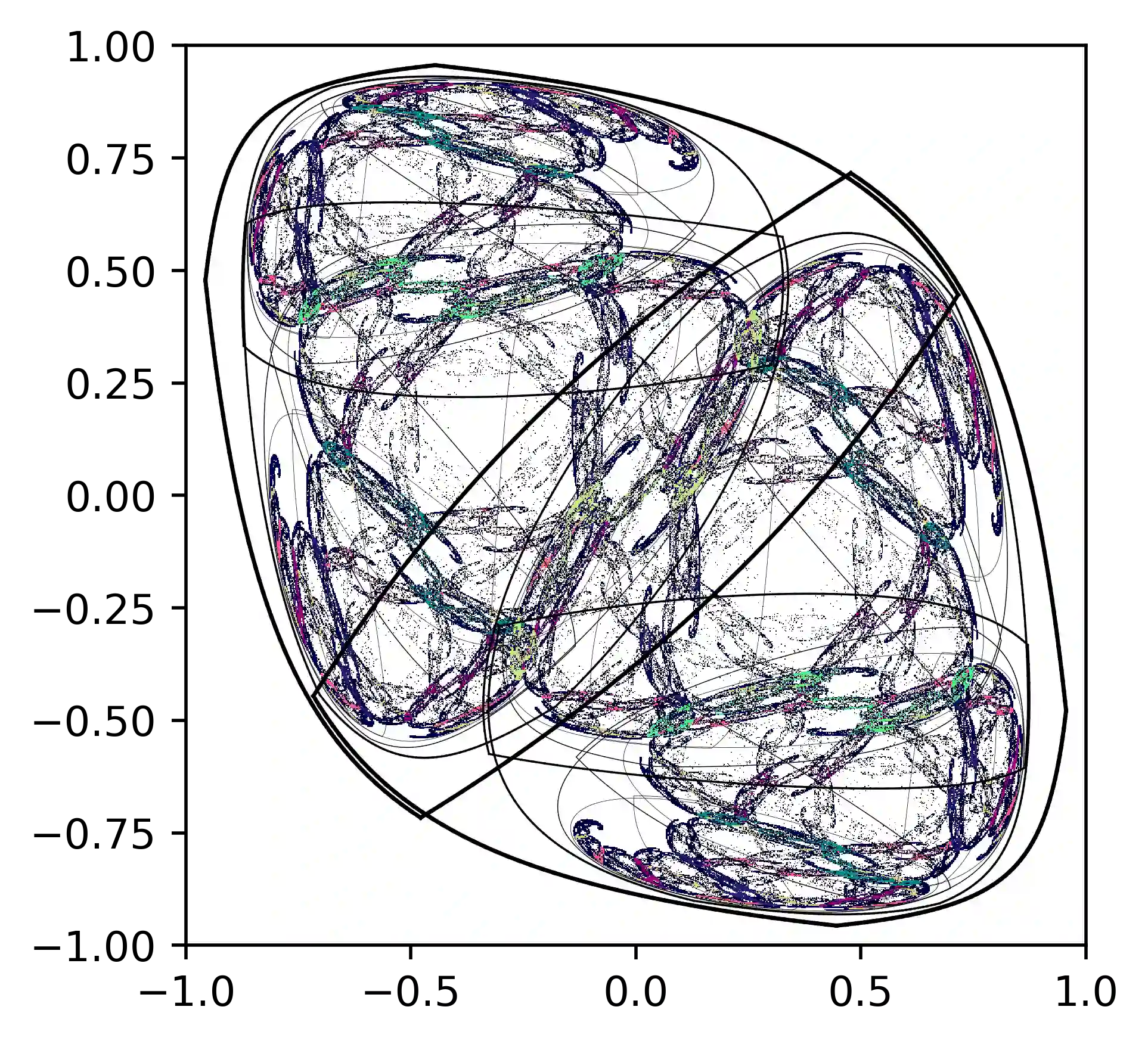
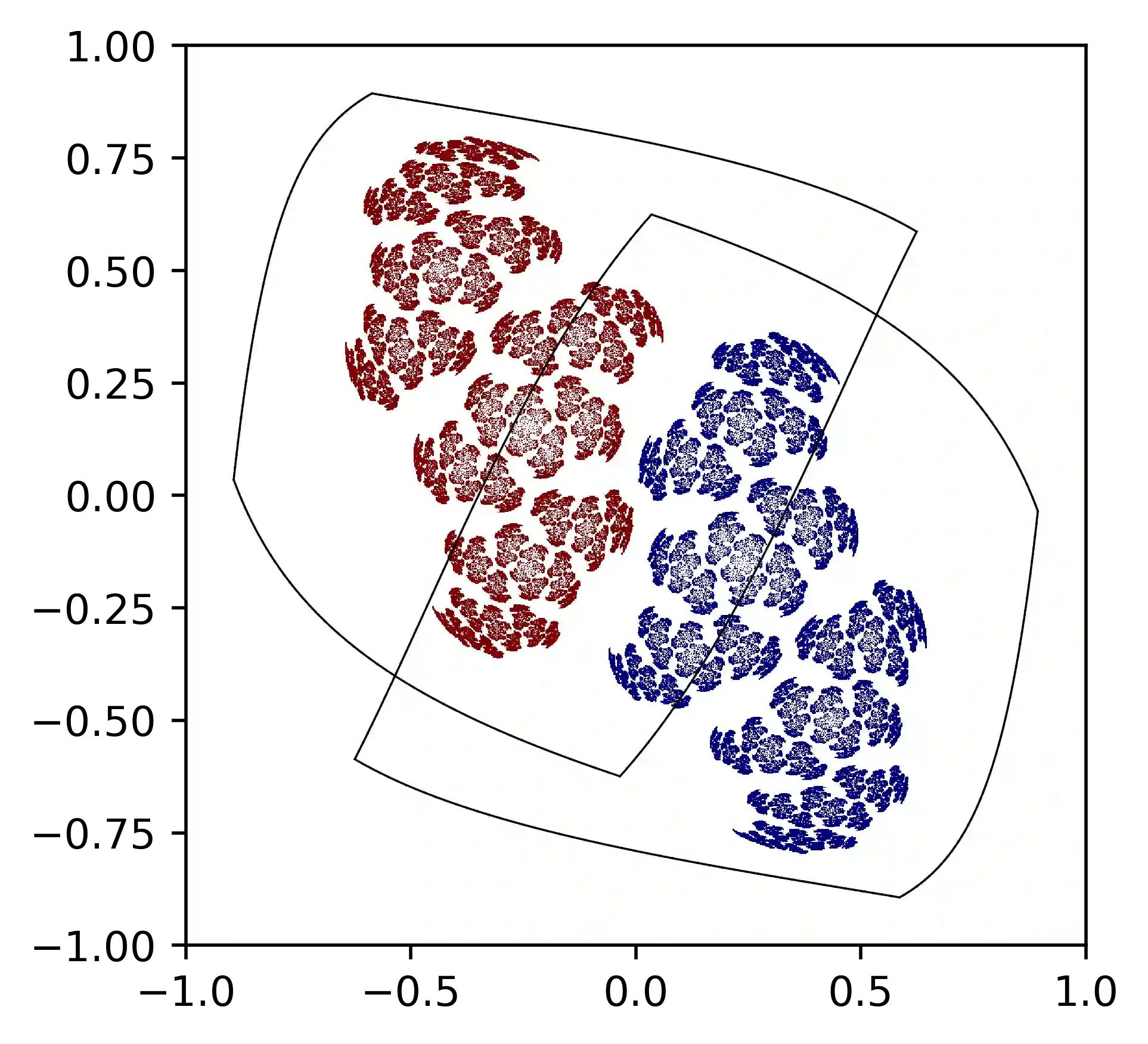
This work joins aspects of reservoir optimization, information-theoretic optimal encoding, and at its center fractal analysis. We build on the observation that, due to the recursive nature of recurrent neural networks, input sequences appear as fractal patterns in their hidden state representation. These patterns have a fractal dimension that is lower than the number of units in the reservoir. We show potential usage of this fractal dimension with regard to optimization of recurrent neural network initialization. We connect the idea of `ideal' reservoirs to lossless optimal encoding using arithmetic encoders. Our investigation suggests that the fractal dimension of the mapping from input to hidden state shall be close to the number of units in the network. This connection between fractal dimension and network connectivity is an interesting new direction for recurrent neural network initialization and reservoir computing.
翻译:这项工作结合了储油层优化、信息理论最佳编码及其中心分形分析的方方面面。 我们以以下观察为基础,即由于经常性神经网络的递归性质,输入序列在其隐藏的状态内呈现成分形模式。 这些模式的分形维度低于储油层中单位的数量。 我们显示了在优化经常性神经网络初始化方面这种分形维度的潜在用途。 我们用算术编码器将“理想”储层的概念与无损最佳编码联系起来。 我们的调查表明,从输入到隐藏状态的绘图的分形维度应接近网络中的单位数量。 分形维度与网络连接之间的这种连接是经常性神经网络初始化和储油层计算的新方向。