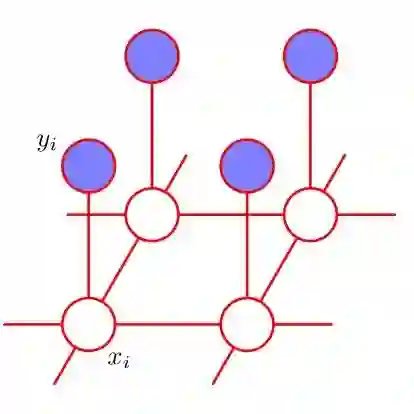
Most popular dimension reduction (DR) methods like t-SNE and UMAP are based on minimizing a cost between input and latent pairwise similarities. Though widely used, these approaches lack clear probabilistic foundations to enable a full understanding of their properties and limitations. To that extent, we introduce a unifying statistical framework based on the coupling of hidden graphs using cross entropy. These graphs induce a Markov random field dependency structure among the observations in both input and latent spaces. We show that existing pairwise similarity DR methods can be retrieved from our framework with particular choices of priors for the graphs. Moreover this reveals that these methods suffer from a statistical deficiency that explains poor performances in conserving coarse-grain dependencies. Our model is leveraged and extended to address this issue while new links are drawn with Laplacian eigenmaps and PCA.
翻译:T-SNE和UMAP等最受欢迎的维度降低(DR)方法,例如 t-SNE和UMAP,其基础是尽量减少投入和潜在相似性之间的成本。这些方法虽然被广泛使用,但缺乏明确的概率基础,无法充分理解其属性和局限性。在这方面,我们引入了一个统一的统计框架,其基础是利用交叉英特罗比将隐藏的图形混合在一起。这些图表在输入和潜在空间的观测中诱发了Markov随机的字段依赖结构。我们显示,现有的双向相似的DR方法可以从我们的框架中检索,并特别选择图表的前缀。此外,这也揭示了这些方法在统计上存在缺陷,从而解释了在保护粗重依赖性方面业绩不佳的原因。我们的模型被利用和扩展来解决这一问题,同时与 Laplecian eigenmaps 和 CPE 建立新的联系。