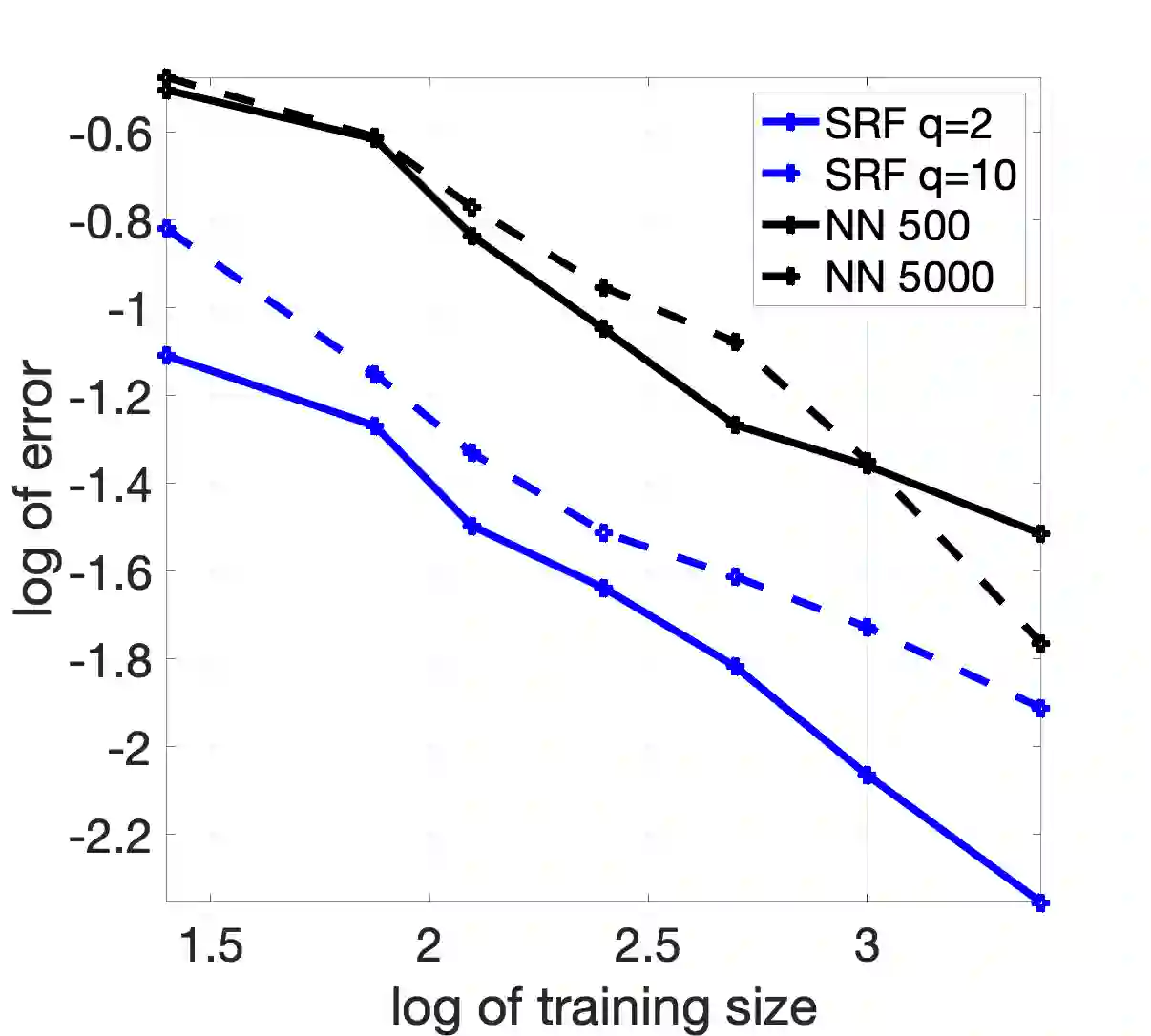
Random feature methods have been successful in various machine learning tasks, are easy to compute, and come with theoretical accuracy bounds. They serve as an alternative approach to standard neural networks since they can represent similar function spaces without a costly training phase. However, for accuracy, random feature methods require more measurements than trainable parameters, limiting their use for data-scarce applications or problems in scientific machine learning. This paper introduces the sparse random feature method that learns parsimonious random feature models utilizing techniques from compressive sensing. We provide uniform bounds on the approximation error for functions in a reproducing kernel Hilbert space depending on the number of samples and the distribution of features. The error bounds improve with additional structural conditions, such as coordinate sparsity, compact clusters of the spectrum, or rapid spectral decay. We show that the sparse random feature method outperforms shallow networks for well-structured functions and applications to scientific machine learning tasks.
翻译:随机特性方法在各种机器学习任务中是成功的,很容易计算,并且具有理论精确度。它们可以作为标准神经网络的替代方法,因为它们可以代表类似的功能空间,而无需经过昂贵的培训阶段。然而,为了准确性,随机特性方法需要比可训练参数更多的测量,限制其用于数据残缺应用或科学机器学习方面的问题。本文介绍了稀有随机特性方法,该方法利用压缩遥感技术来学习有腐蚀性的随机特性模型。我们根据样品数量和特征分布,为再生产内核Hilbert空间的功能提供了近似误差的统一界限。错误界限随着额外的结构条件而改善,如坐标宽度、频谱集集或光谱快速衰减。我们显示,稀有随机特性方法比浅网络更形,用于结构完善的功能和应用到科学机器学习任务。