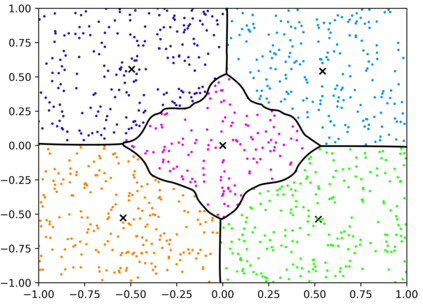
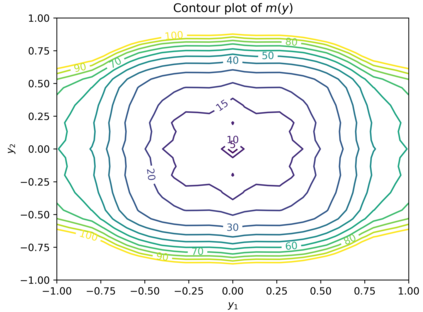
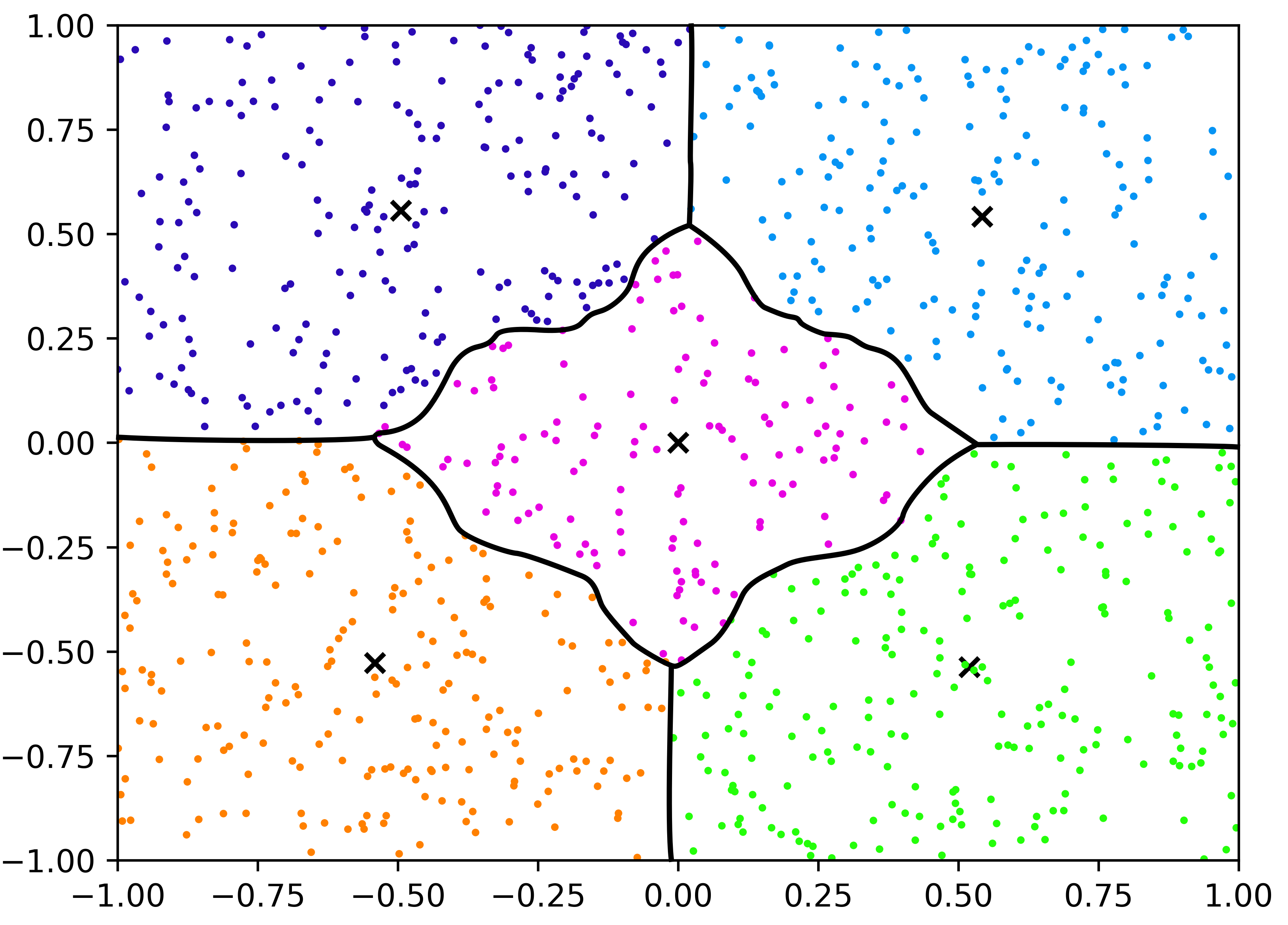
In this work, we address the efficient computation of parameterized systems of linear equations, with possible nonlinear parameter dependence. When the matrix is highly sensitive to the parameters, mean-based preconditioning might not be enough. For this scenario, we explore an approach in which several preconditioners are placed in the parameter space during a precomputation step. To determine the optimal placement of a limited number of preconditioners, we estimate the expected number of iterations with respect to a given preconditioner a priori and use a location-allocation strategy to optimize the placement of the preconditioners. We elaborate on our methodology for the Helmholtz problem with exterior Dirichlet scattering at high frequencies, and we estimate the expected number of GMRES iterations via a gray-box Gaussian process regression approach. We illustrate our approach in two practical applications: scattering in a domain with a parametric refractive index and scattering from a scatterer with parameterized shape. Using these numerical examples, we show how our methods leads to runtime savings of about an order of magnitude. Moreover, we investigate the effect of the parameter dimension and the importance of dimension anisotropy on their efficacy.
翻译:暂无翻译