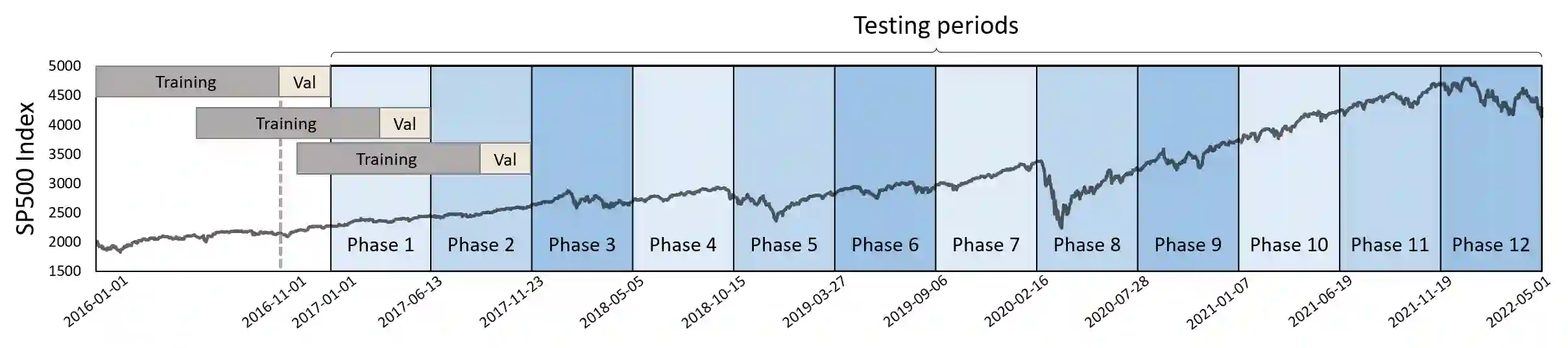
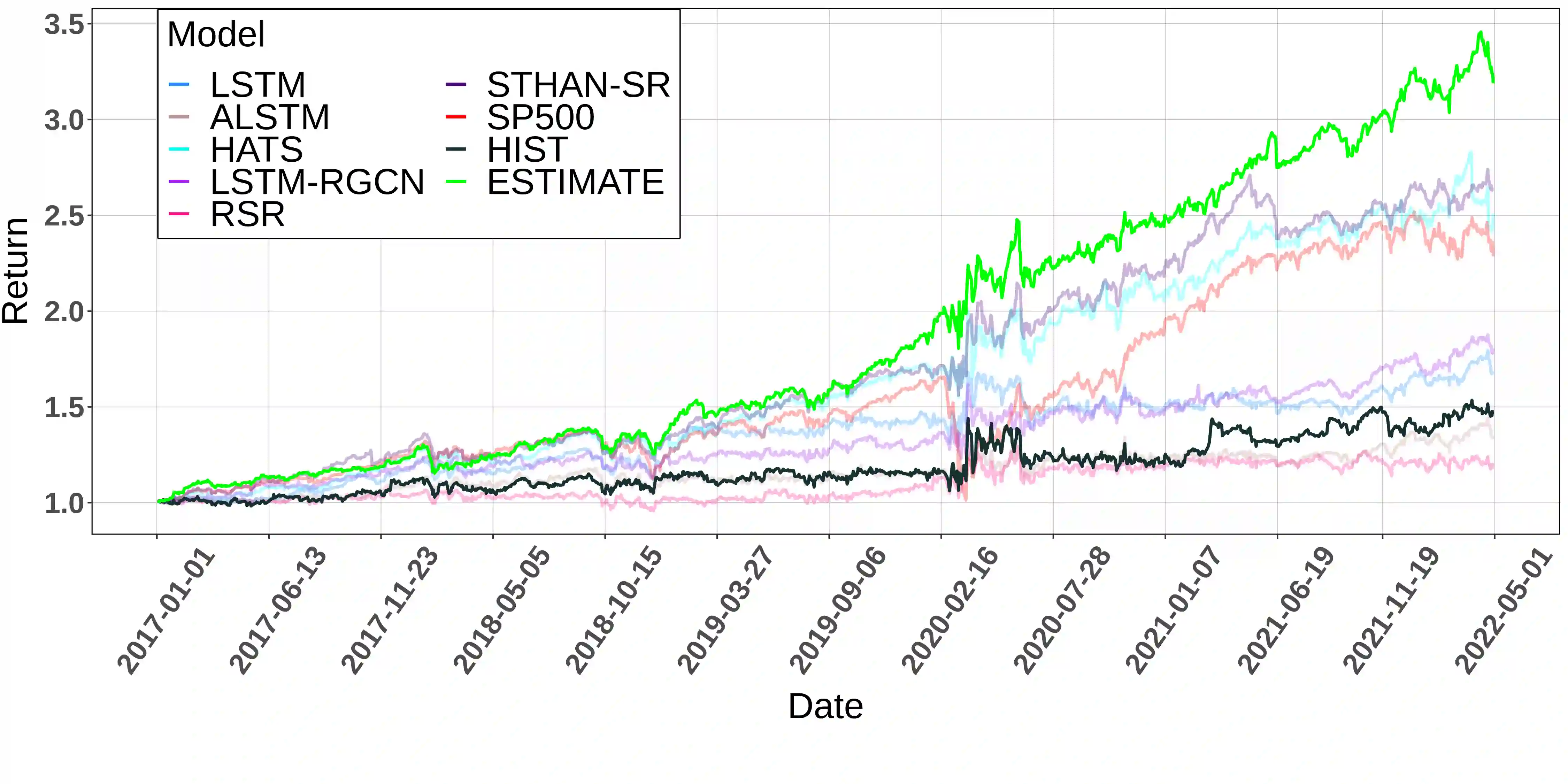
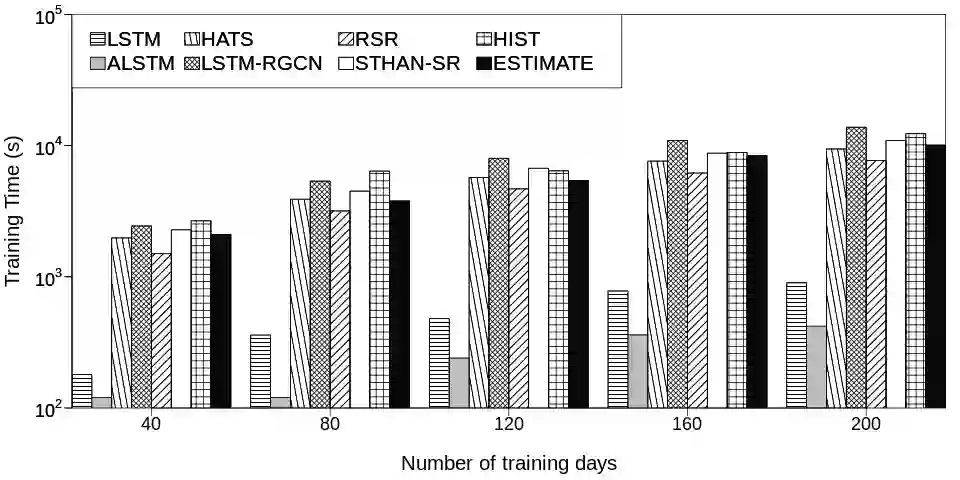
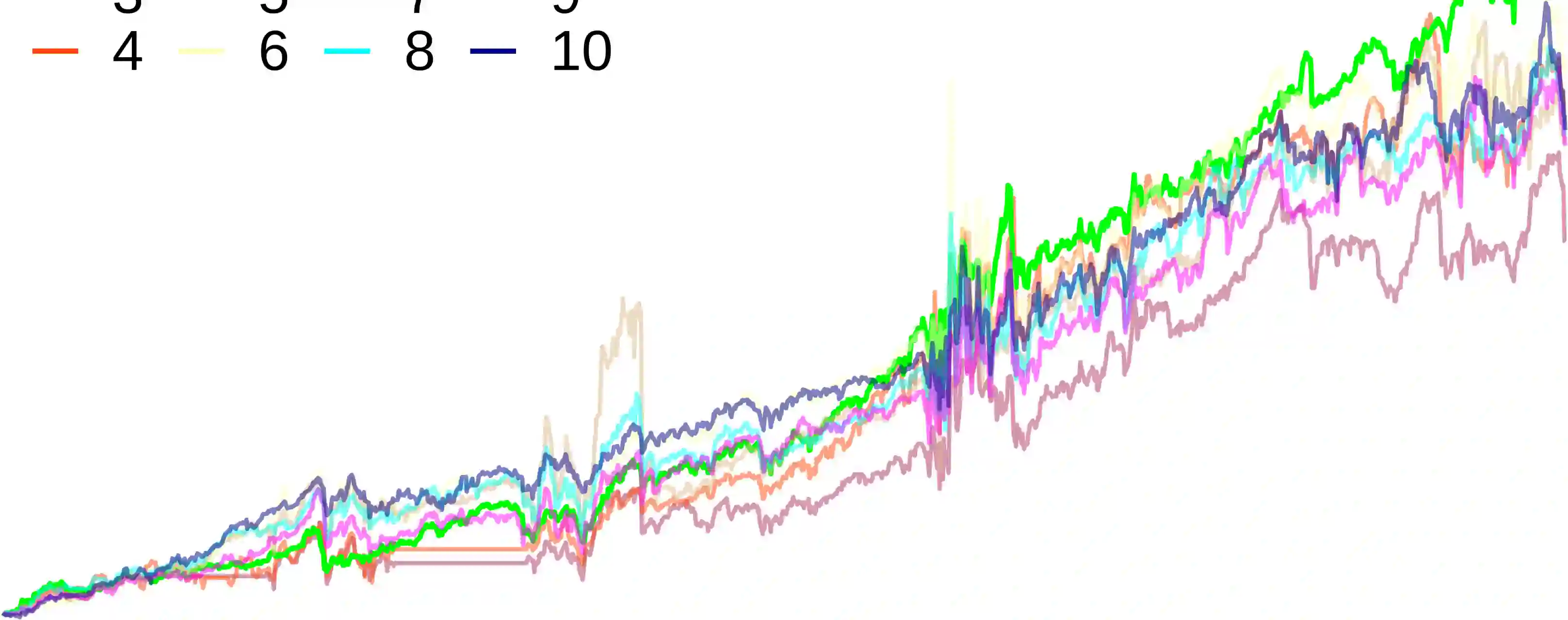
Advances in deep neural network (DNN) architectures have enabled new prediction techniques for stock market data. Unlike other multivariate time-series data, stock markets show two unique characteristics: (i) \emph{multi-order dynamics}, as stock prices are affected by strong non-pairwise correlations (e.g., within the same industry); and (ii) \emph{internal dynamics}, as each individual stock shows some particular behaviour. Recent DNN-based methods capture multi-order dynamics using hypergraphs, but rely on the Fourier basis in the convolution, which is both inefficient and ineffective. In addition, they largely ignore internal dynamics by adopting the same model for each stock, which implies a severe information loss. In this paper, we propose a framework for stock movement prediction to overcome the above issues. Specifically, the framework includes temporal generative filters that implement a memory-based mechanism onto an LSTM network in an attempt to learn individual patterns per stock. Moreover, we employ hypergraph attentions to capture the non-pairwise correlations. Here, using the wavelet basis instead of the Fourier basis, enables us to simplify the message passing and focus on the localized convolution. Experiments with US market data over six years show that our framework outperforms state-of-the-art methods in terms of profit and stability. Our source code and data are available at \url{https://github.com/thanhtrunghuynh93/estimate}.
翻译:与其它多变时间序列数据不同,股票市场显示出两个独特的特征:(一) emph{多序列动态},因为股票价格受到强大的非双向关系的影响(例如同一行业内部);和(二) emph{内部动态},因为每个股票都表现出某种特殊行为。最近基于DNN{内部的系统方法利用高压图谱捕捉了多级动态,但依赖Freier基础的多级关系。此外,股票市场在很大程度上忽略了内部动态,对每股采用相同的模型,这意味着严重的信息损失。在本文中,我们提出了一个股票流动预测框架,以克服上述问题。具体地说,该框架包括时间型基因过滤器,在LSTM网络上安装基于记忆的机制,以学习每个股票的单个模式。此外,我们使用高调关注点来捕捉非双向关系,而两者都是低效的。在这里,使用恒波基础而不是四州级标准基,使用在线基准,让我们的市场稳定度数据在六年中展示。