Shift of Pairwise Similarities for Data Clustering

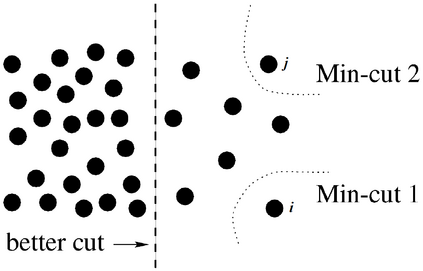
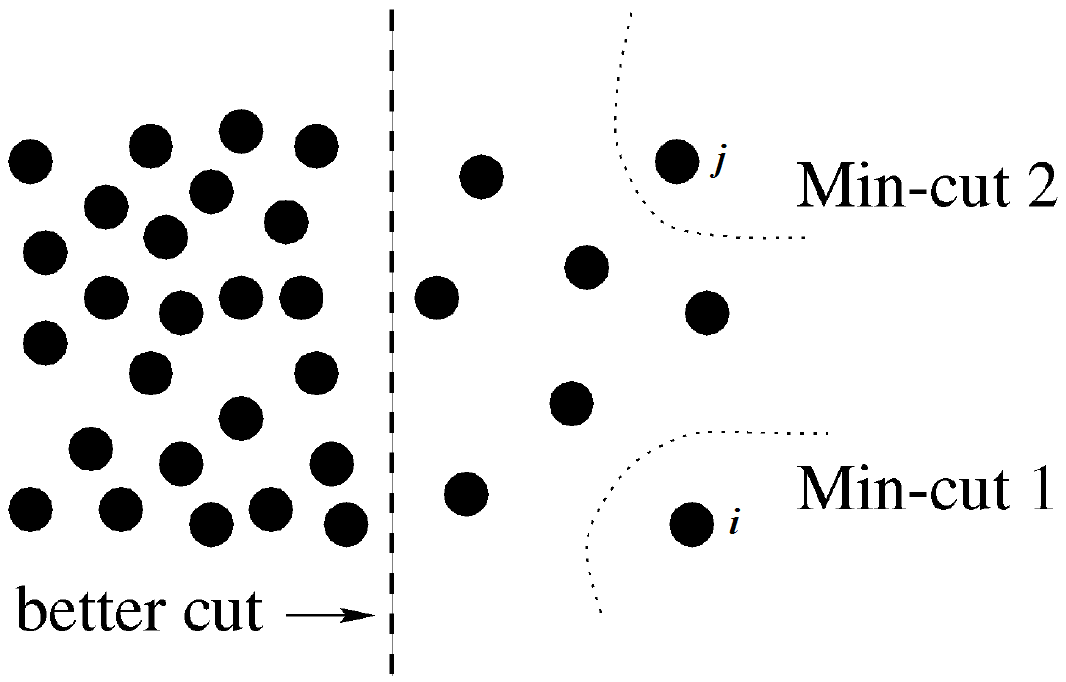
Several clustering methods (e.g., Normalized Cut and Ratio Cut) divide the Min Cut cost function by a cluster-dependent factor (e.g., the size or the degree of the clusters), in order to yield a more balanced partitioning. We, instead, investigate adding such regularizations to the original cost function. We first consider the case where the regularization term is the sum of the squared size of the clusters, and then generalize it to adaptive regularization of the pairwise similarities. This leads to shifting (adaptively) the pairwise similarities which might make some of them negative. We then study the connection of this method to Correlation Clustering and then propose an efficient local search optimization algorithm with fast theoretical convergence rate to solve the new clustering problem. In the following, we investigate the shift of pairwise similarities on some common clustering methods, and finally, we demonstrate the superior performance of the method by extensive experiments on different datasets.