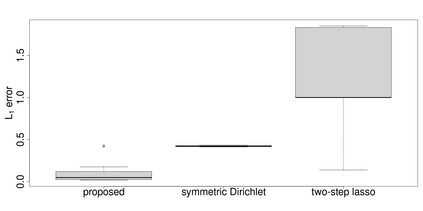
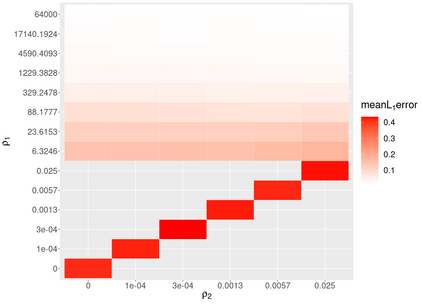
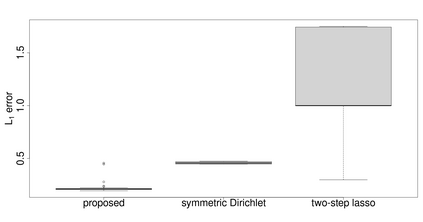
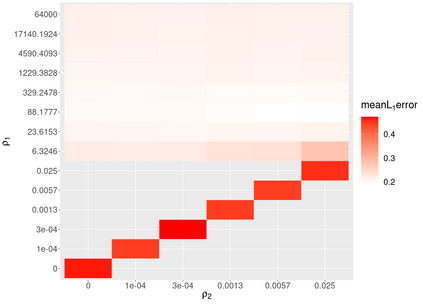
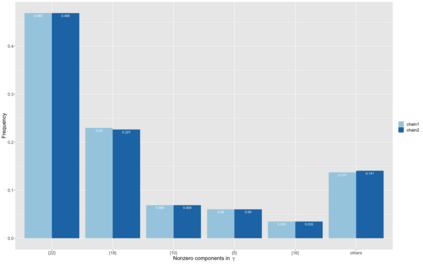
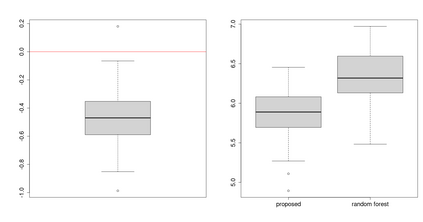
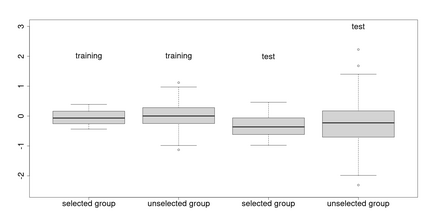
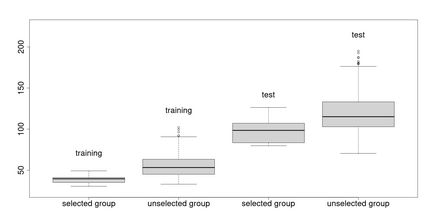
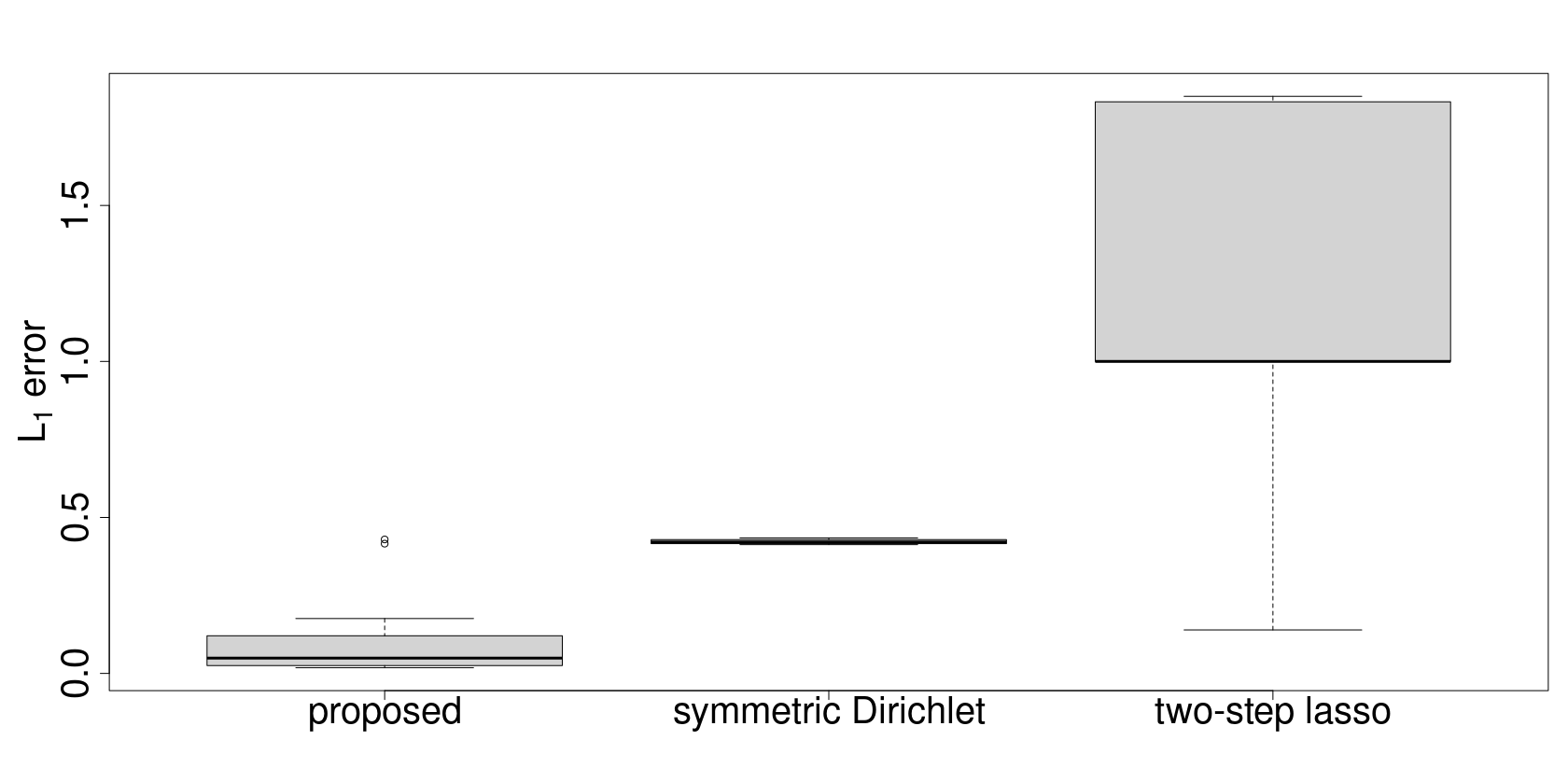
Assigning weights to a large pool of objects is a fundamental task in a wide variety of applications. In this article, we introduce the concept of structured high-dimensional probability simplexes, in which most components are zero or near zero and the remaining ones are close to each other. Such structure is well motivated by (i) high-dimensional weights that are common in modern applications, and (ii) ubiquitous examples in which equal weights -- despite their simplicity -- often achieve favorable or even state-of-the-art predictive performance. This particular structure, however, presents unique challenges partly because, unlike high-dimensional linear regression, the parameter space is a simplex and pattern switching between partial constancy and sparsity is unknown. To address these challenges, we propose a new class of double spike Dirichlet priors to shrink a probability simplex to one with the desired structure. When applied to ensemble learning, such priors lead to a Bayesian method for structured high-dimensional ensembles that is useful for forecast combination and improving random forests, while enabling uncertainty quantification. We design efficient Markov chain Monte Carlo algorithms for implementation. Posterior contraction rates are established to study large sample behaviors of the posterior distribution. We demonstrate the wide applicability and competitive performance of the proposed methods through simulations and two real data applications using the European Central Bank Survey of Professional Forecasters data set and a data set from the UC Irvine Machine Learning Repository (UCI).
翻译:将重力指派给大型天体库是多种应用中的一项基本任务。 在本条中, 我们引入了结构化高维概率简单度概念, 大部分部件为零或接近零, 其余的部件彼此接近。 这种结构的动机是:(一) 在现代应用中常见的高维重量, 以及(二) 各种例子, 等量( 尽管它们简单, 却往往能够取得优异甚至最先进的高级的预测性能) 。 然而, 这一特殊结构带来了独特的挑战, 部分原因是, 与高维线性线性回归不同, 参数空间是一个简单x和模式的转换, 在部分趋同性和宽度之间是未知的。 为了应对这些挑战, 我们提出一个新的等级是双倍加点Drichlet, 将概率简单到一个, 与理想的结构相匹配。 当应用于“ 感官学习” 时, 此类前几个例子导致一种巴耶斯的系统方法, 用于预测组合和改进随机森林, 同时, 使得不确定性的量化。 我们设计了一个高效的Markov 链 的竞争性应用性和模式, 在部分相异性应用Recar Carlooalal Adal 数据序列中, 将数据排序用于执行。