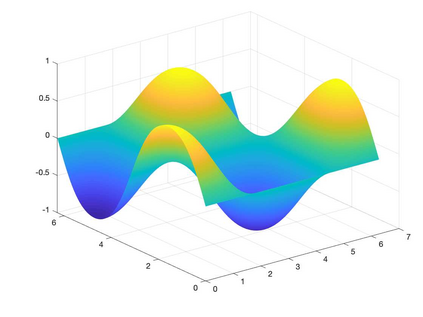
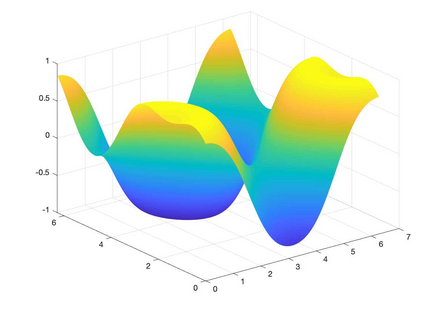
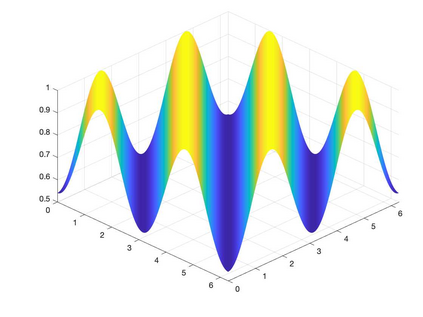
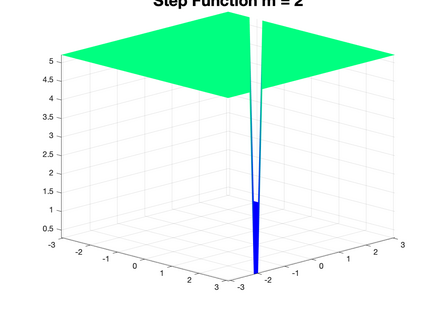
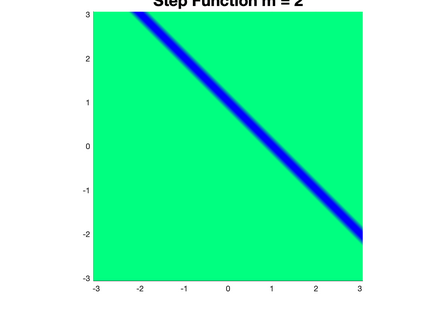
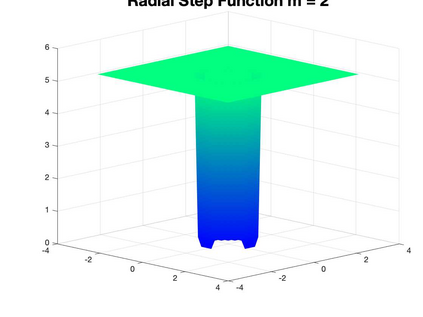
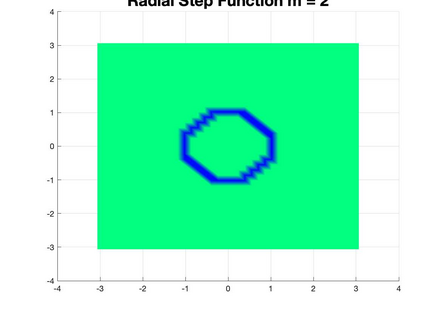
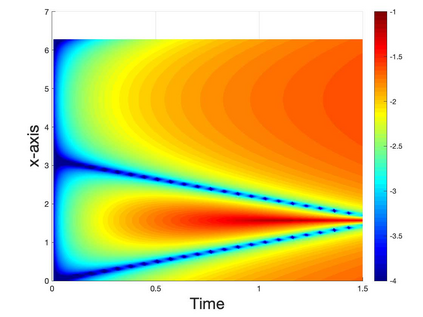
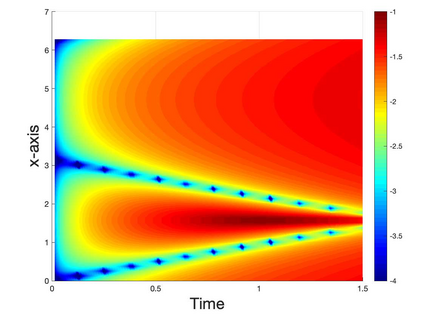
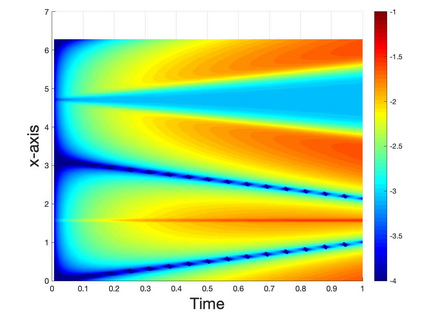
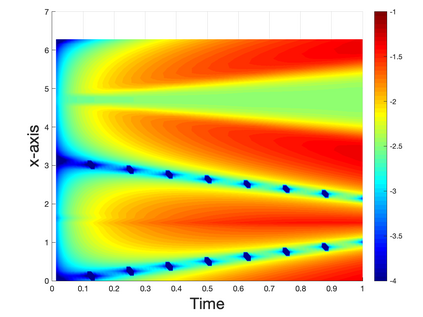
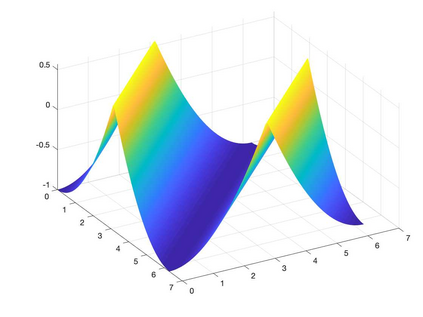
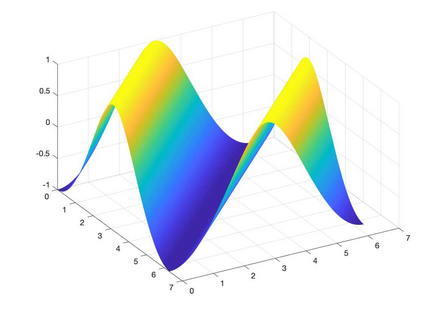
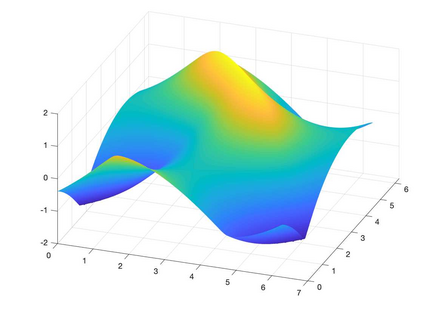
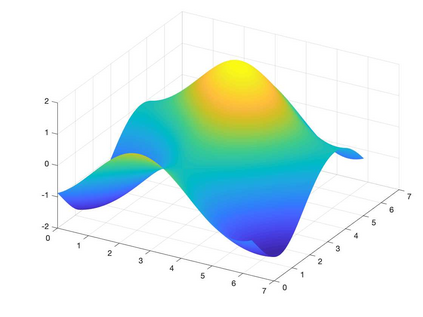
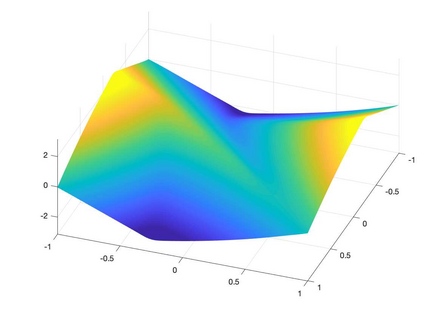
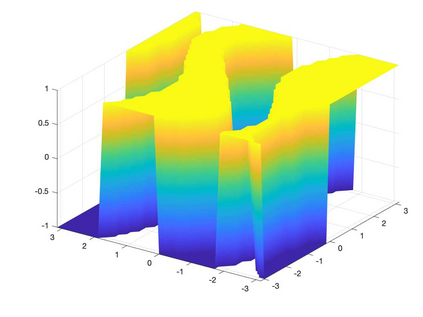
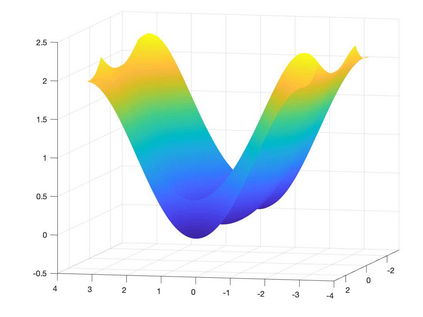
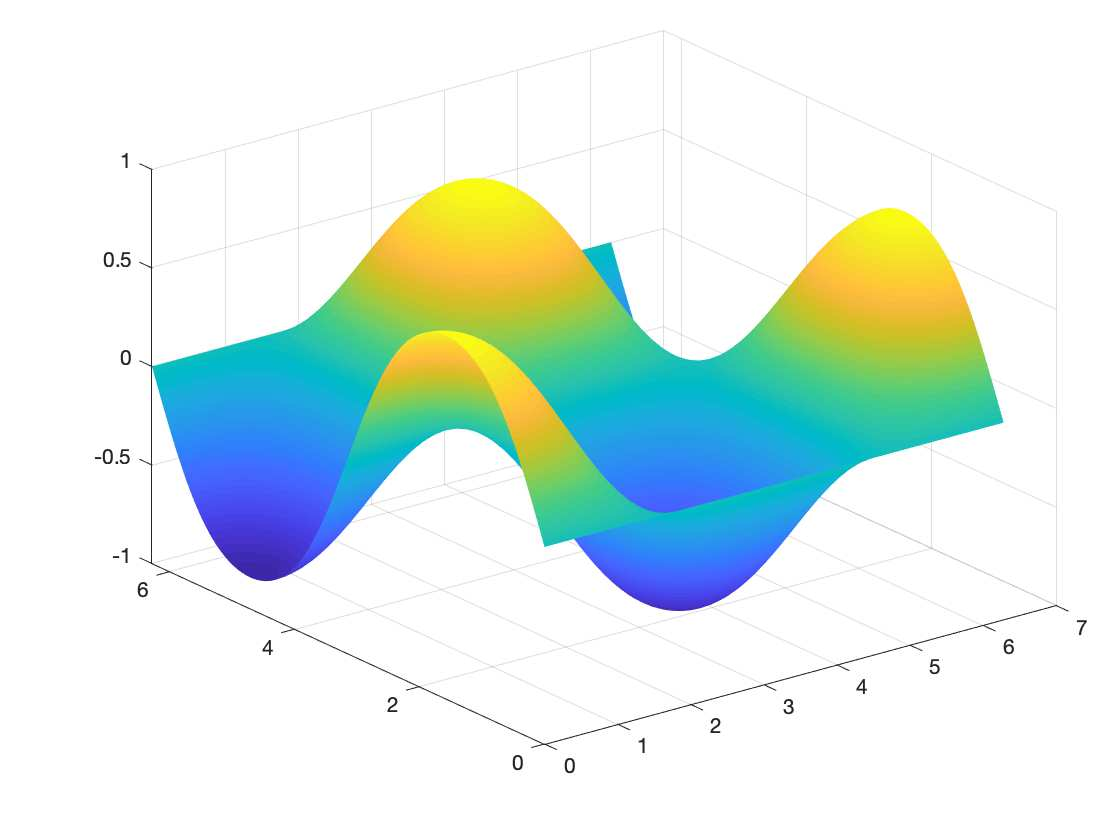
We present a Hermite interpolation based partial differential equation solver for Hamilton-Jacobi equations. Many Hamilton-Jacobi equations have a nonlinear dependency on the gradient, which gives rise to discontinuities in the derivatives of the solution, resulting in kinks. We built our solver with two goals in mind: 1) high order accuracy in smooth regions and 2) sharp resolution of kinks. To achieve this, we use Hermite interpolation with a smoothness sensor. The degrees-of freedom of Hermite methods are tensor-product Taylor polynomials of degree $m$ in each coordinate direction. The method uses $(m+1)^d$ degrees of freedom per node in $d$-dimensions and achieves an order of accuracy $(2m+1)$ when the solution is smooth. To obtain sharp resolution of kinks, we sense the smoothness of the solution on each cell at each timestep. If the solution is smooth, we march the interpolant forward in time with no modifications. When our method encounters a cell over which the solution is not smooth, it introduces artificial viscosity locally while proceeding normally in smooth regions. We show through numerical experiments that the solver sharply captures kinks once the solution losses continuity in the derivative while achieving $2m+1$ order accuracy in smooth regions.
翻译:我们为汉密尔顿-贾科比方程式展示了基于部分差异方程式的Hermite内插法。 许多汉密尔顿-贾科比方程式对梯度有非线性依赖性,导致解决方案衍生物的不连续性,导致偏差。 我们构建了我们的解决方案有两个目标:(1) 平滑地区的高度秩序准确性,(2) 直截了当的离子解。 为了实现这一点,我们用一个平滑的传感器来使用Hermite内插法。 赫米特方法的自由度是每个坐标方向的Taylor产品多级多价米。 当我们的方法遇到一个解决方案平滑的单元格时, 每节点使用$(m+1)d$(每个节点的自由度),导致问题衍生物的不连续性,当解决方案平滑时,我们用美元(2m+1)构建一个准确度的精确度。 为了清晰地解决每个单元格的平滑度,我们感到解决方案的平滑性,我们不作任何改动地前进。 当我们的方法遇到一个解决方案是平滑的单元格时, 当我们找到一个解决方案是平滑的单元格时, 平滑的,我们通常通过平滑的平流的平流的平流的平流的平流 。