Coded Caching for Two-Dimensional Multi-Access Networks

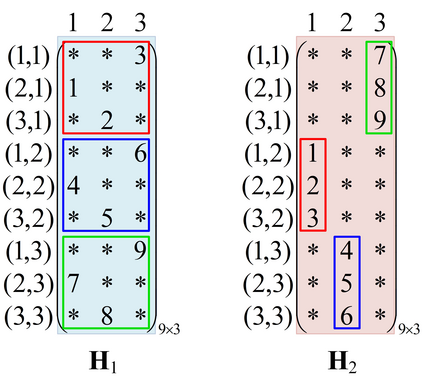
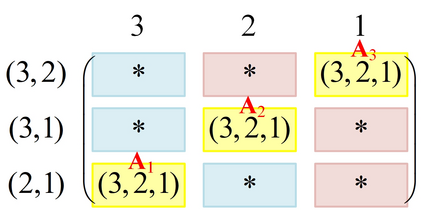
This paper studies a novel multi-access coded caching (MACC) model in two-dimensional (2D) topology, which is a generalization of the one-dimensional (1D) MACC model proposed by Hachem et al. We formulate a 2D MACC coded caching model, formed by a server containing $N$ files, $K_1\times K_2$ cache-nodes with limited memory $M$ which are placed on a grid with $K_1$ rows and $K_2$ columns, and $K_1\times K_2$ cache-less users such that each user is connected to $L^2$ nearby cache-nodes. More precisely, for each row (or column), every user can access $L$ consecutive cache-nodes, referred to as row (or column) 1D MACC problem in the 2D MACC model. The server is connected to the users through an error-free shared link, while the users can retrieve the cached content of the connected cache-nodes without cost. Our objective is to minimize the worst-case transmission load among all possible users' demands. In this paper, we propose a baseline scheme which directly extends an existing 1D MACC scheme to the 2D model by using a Minimum Distance Separable (MDS) code, and two improved schemes. In the first scheme referred to as grouping scheme, which works when $K_1$ and $K_2$ are divisible by $L$, we partition the cache-nodes and users into $L^2$ groups according to their positions, such that no two users in the same group share any cache-node, and we utilize the seminal shared-link coded caching scheme proposed by Maddah-Ali and Niesen for each group. Subsequently, for any model parameters satisfying $\min\{K_1,K_2\}>L$ we propose the second scheme, referred to as hybrid scheme, consisting in a highly non-trivial way to construct a 2D MACC scheme through a vertical and a horizontal 1D MACC schemes.