Normalizing Flows入门(上)

2020 年 8 月 1 日 AINLP

Normalizing Flows入门(上)

标准化流能做什么？假设我们想生成人脸，但我们并不知道人脸图片在高维空间D的分布，我可以用一个简单的分布pz，从中sample出一个向量z，让它通过标准化流，得到一个新的向量x，让x的分布与人脸的分布相近，这样我们就可以生成任意张不同的人脸照片。

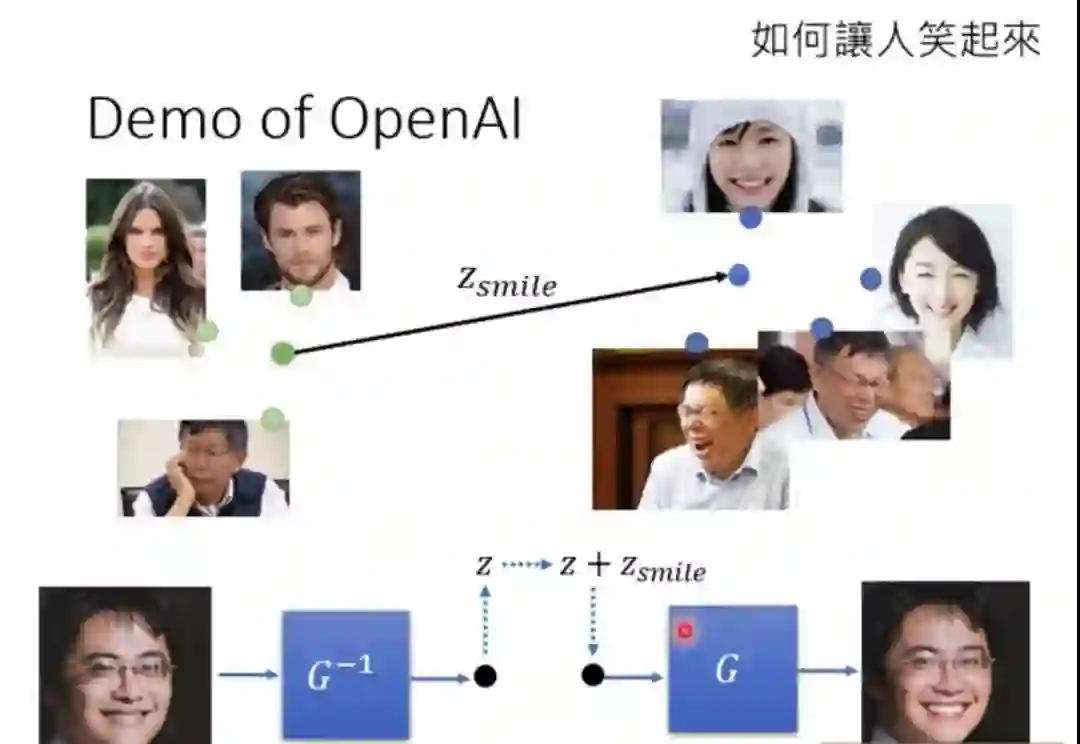
再举一个例子，如果我们有一堆冷漠脸的图片，和一堆笑脸的图片，把多张冷漠脸通过逆标准化流，取平均得到一个向量z1，再把多张笑脸通过逆标准化流，取平均得到向量z2，用z2减去z1得到z3，z3应该就是在z空间中，从冷漠脸区域指向笑脸区域的向量，那我们现在把任意一个冷漠脸的人的图片x拿来通过逆标准化流得到z4，令z5 = z3 + z4，再通过标准化流应该就可以得到这个人笑脸样子的图片了！

李宏毅老师说flow-based model虽然效果不错，但是没有VAE和GAN有名的原因可能是因为它的数学太多，导致用的人不多hhh

1. 前置知识

标准化流(Normalizing Flow)能够将简单的概率分布转换为极其复杂的概率分布，可以用在生成式模型、强化学习、变分推断等领域，构建它所需要的工具是：行列式(Determinant)、雅可比矩阵(Jacobi)、变量替换定理(Change of Variable Theorem)，下面先简单介绍这三个工具。

1.1 行列式

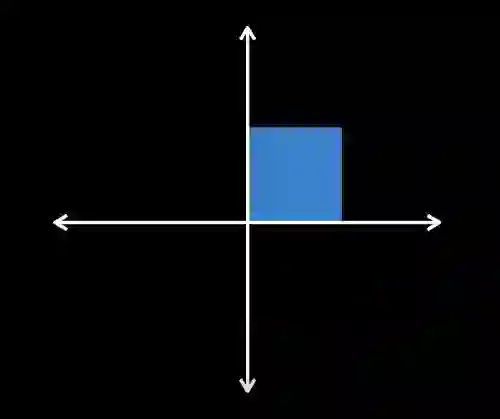
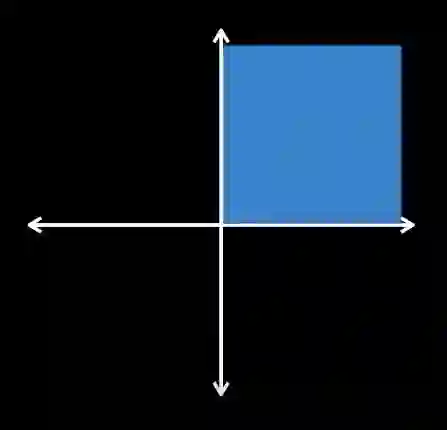
行列式的求法不再赘述，我们主要需要理解的是行列式的物理意义。一个矩阵的行列式的值表示的是该矩阵对空间所做的变换，将原来的空间放大或缩小了多少倍，比如二维空间在原点有一个边长为1的正方形a，对它做变换得到新的正方形b，，，新的正方形边长被放大为原来的2倍，面积为原来的4倍，，

三维以及更高维空间亦同理

1.2 雅可比矩阵

设有一个二维向量，给定变换，，那么变换的雅可比矩阵

变换的逆变换，，的雅可比矩阵

可以发现与互为逆矩阵，事实上互为逆变换的与，其二者对应的雅可比矩阵也互为逆阵，因此又由行列式的性质可得它们的雅可比行列式互为倒数，即

变换可以不仅仅是矩阵变换，也可以任意的函数，将D维的向量变换为D'维的，。

1.3 Change of Variable Theorem

假设有一变量，服从分布，有一变换，，是已知的一种简单分布，变换可逆，且与都可微分，现在要求，即随机变量的概率密度函数，因为概率之和相等

假设x和z都是在整个空间上积分，那么被积分的部分绝对值必定处处相等，由于概率p必大于等于0，可去掉其两边的绝对值号，即得

第(8)式也可写为

(5)~(8)式的直观理解：两边都是概率密度乘以空间的大小，得到是一个标量，即随机变量落在该空间的概率大小，将变换写入，即将其写为，但x为向量而非标量，这里要表示的是空间变化的大小关系，我们由雅可比矩阵的定义可知，又由行列式的物理意义，知道的绝对值为将z映射到x时，空间大小放缩的倍数，即为概率密度放缩的倍数倒数，又因，因此可得(8)式。

在论文中解释大意是：「我们可以认为T在通过expand或contract R^D空间来使得pz变得和px相近。雅可比行列式detT的绝对值量化了原向量z附近的体积由于经过T变换后，体积相对变化的大小，即当z附近一块无穷小的体积dz，经过T后被map到了x附近的一块无穷小的体积dx处，那么detT等于dx除以dz，即映射后的体积是原来的几倍，因为dz中包含的概率等于dx中包含的概率，因此如果dz的体积被放大了，那么dx里的概率密度应该缩小」

举个例子，假设随机变量z属于0-1均匀分布，在取值空间 =(0, 1)上，p(z)=1，有变换T，T(z)=2z，令x=T(z)，则x必是 =(0, 2)上的均匀分布，但此时p(x)不再是1了，否则在(0, 2)上都有p(x)=1，积分可得概率之和为2，明显错误，因为变换T将原空间中z可取值的范围放大了一倍，从(0, 1)变为了(0, 2)，即可取值空间从变为，空间放大的倍数为，那概率密度缩小的倍数为，即相应的x概率密度应该缩小一倍，因此

2. 标准化流的定义和基础

我们的目标是使用简单的概率分布来建立我们想要的更为复杂更有表达能力的概率分布，使用的方法就是Normalizing Flow，flow的字面意思是一长串的T，即很多的transformation。让简单的概率分布，通过这一系列的transformation，一步一步变成complex、expressive的概率分布，like a fluid flowing through a set of tubes，fluid就是说概率分布像水一样，是可塑的易变形的，我们把它通过一系列tubes，即变换T们，塑造成我们想要的样子——最终的概率分布。下面开始使用的符号尽量与原论文保持一致。

2.1 Normalizing Flow’s properties

x与u必须维度相同，因为只有维度相同，下面的变换T才可能可逆
变换T必须可逆，且T和T的逆必须可导
变换T可以由多个符合条件2的变换Ti组合而成

从使用角度来说，一个flow-based model提供了两个操作，一是sampling，即从pu中sample出u，经过变换T得到x，，另一个是evaluating模型的概率分布，使用公式。

两种操作有不同的计算要求，sampling需要能够sample from pu 以及计算变换T，evaluating需要能够计算T的逆与雅可比行列式，并evaluate pu，因此计算时的效率与难度对应用来说至关重要

2.2 Flow-based models有多强的表达能力？

我们知道p(u)是很简单的一个概率分布，那么通过flow，我们能将p(u)转换为任意的概率分布p(x)吗？假设x为D维向量，p(x)>0，的概率分布只依赖i之前的元素，那么可以将分解为条件概率的乘积

假设变换F将x映射为z，zi的值由xi的累积分布函数(cdf)确定

很明显F是可微分的，其微分就等于，由于Fi对xj的偏微分当j > i时等于0，因此是一个下三角矩阵，那么其行列式就等于其对角线元素的乘积，即

由于p(x)>0，所以雅可比行列式也>0，那么变换F的逆必存在，由(9)式，将x与z对调，T改为F，可得

即z是D维空间中(0, 1)之间的均匀分布。

上述对p(x)的限制仅仅是依赖于的条件概率对可微，且，我们就使用变换F将它变为了最简单的(0, 1)均匀分布，又因为F可逆，所以我们可以使用F的逆将p(z)转换为任意满足上述条件的概率分布p(x)。我们再推广到任意的base distribution，假设p(u)满足上述p(x)满足的条件，那么我们可以使用变换G将任意的概率分布p(u)转换为p(z)，再用F逆将p(z)转换为任意的概率分布p(x)，即使用变换，可将变为。

2.3 使用flows来建模和推断

为了拟合一个概率模型，我们要拟合一个flow-based model 去近似目标分布，代表，和分别是T与p(u)的参数，可以通过最小化KL散度和最大似然估计做到

2.3.1 正向KL散度与最大似然估计

假设现在我们手上有N条真实的数据，即来自于的samples，那么可以使用蒙特卡罗法来近似上面的期望值

最小化上式等价于求模型在该N条数据上的最大似然估计，我们一般使用随机梯度下降来优化上式的参数。

可见，为了使用正向KL散度或最大似然估计来拟合目标分布，我们需要计算、它的雅可比行列式， evaluate base分布，以及关于它们参数的导数。

2.3.2 反向KL散度

当我们能够计算T，它的雅可比行列式，evaluate 目标分布p*以及从p(u)中sample时，使用反向KL散度是合适的，事实上，即使我们只能evaluate 目标分布乘以某个正则化常数，也可以最小化上式，，是一个更好处理的概率分布，重写上式为

当我们有N条来自于的samples，为了最小化上式，使用蒙特卡罗法，并对变换T的参数求偏导，可得

未完待续，如何构建Normalizing flow将在中篇和下篇介绍

推荐阅读

文心（ERNIE）3项能力助力快速定制企业级NLP模型，EasyDL全新升级！

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。