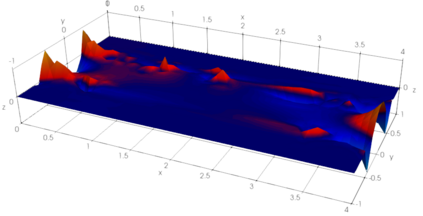
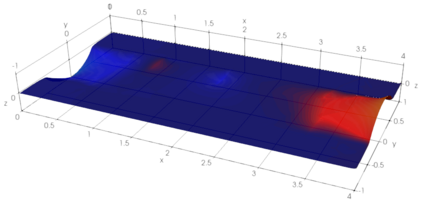
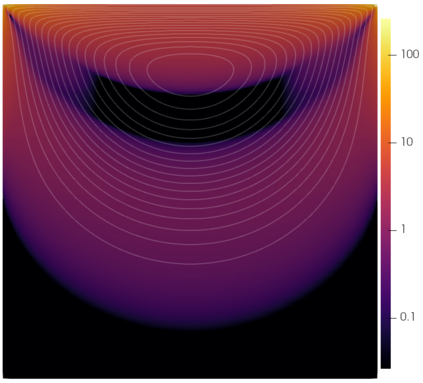
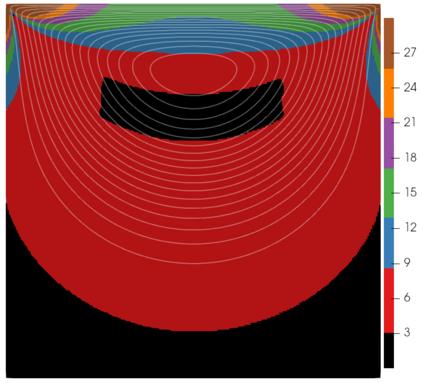
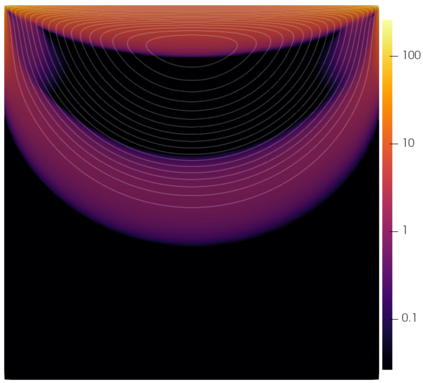
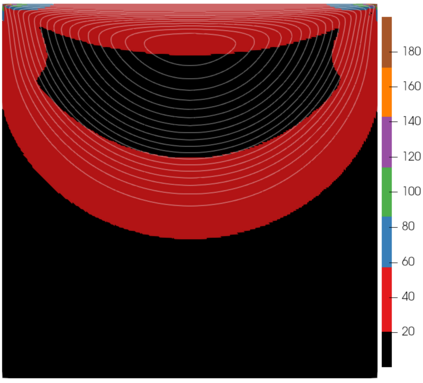
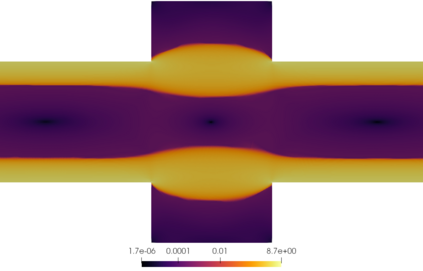
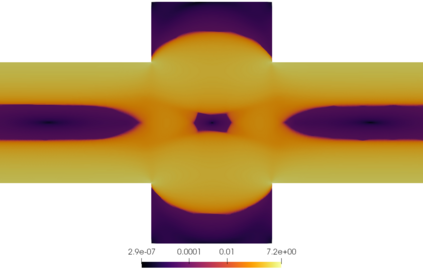
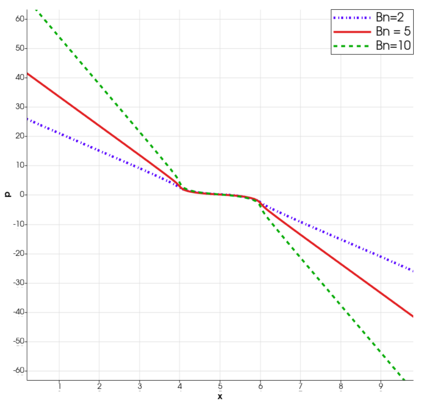
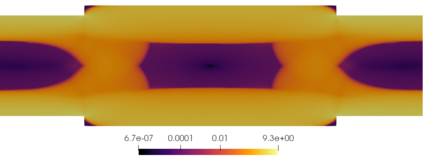
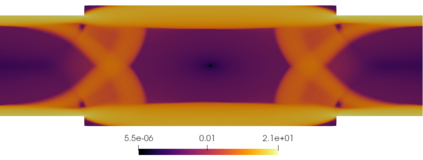
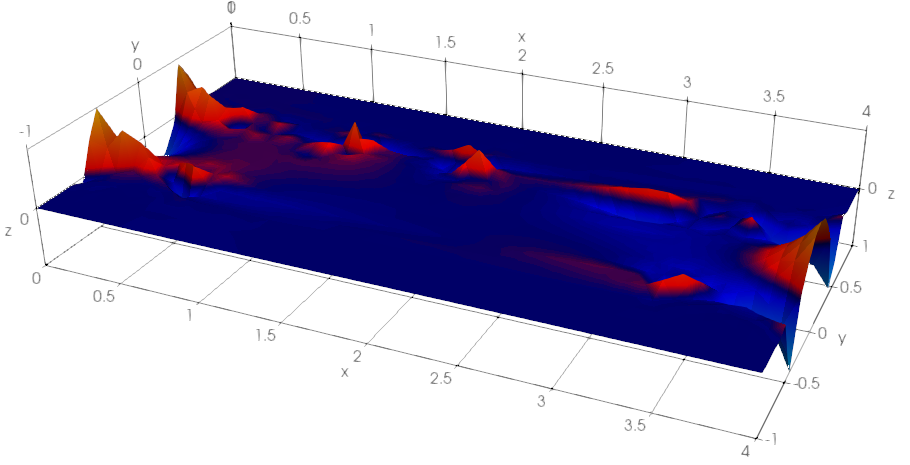
We propose a semismooth Newton method for non-Newtonian models of incompressible flow where the constitutive relation between the shear stress and the symmetric velocity gradient is given implicitly; this class of constitutive relations captures for instance the models of Bingham and Herschel-Bulkley. The proposed method avoids the use of variational inequalities and is based on a particularly simple regularisation for which the (weak) convergence of the approximate stresses is known to hold. The system is analysed at the function space level and results in mesh-independent behaviour of the nonlinear iterations.
翻译:我们建议对非纽顿式的不可压缩流动模型采用半斯摩特牛顿法,其中隐含了剪裁应力和对称速度梯度之间的构成关系;这种构成关系类别包括了宾汉姆和赫尔歇尔-布尔克利的模式;拟议方法避免了差异性不平等的使用,并基于一种特别简单的常规化,已知约合应力的(弱的)趋同将保持。该系统在功能空间层面进行分析,并导致非线性迭代的网状独立行为。