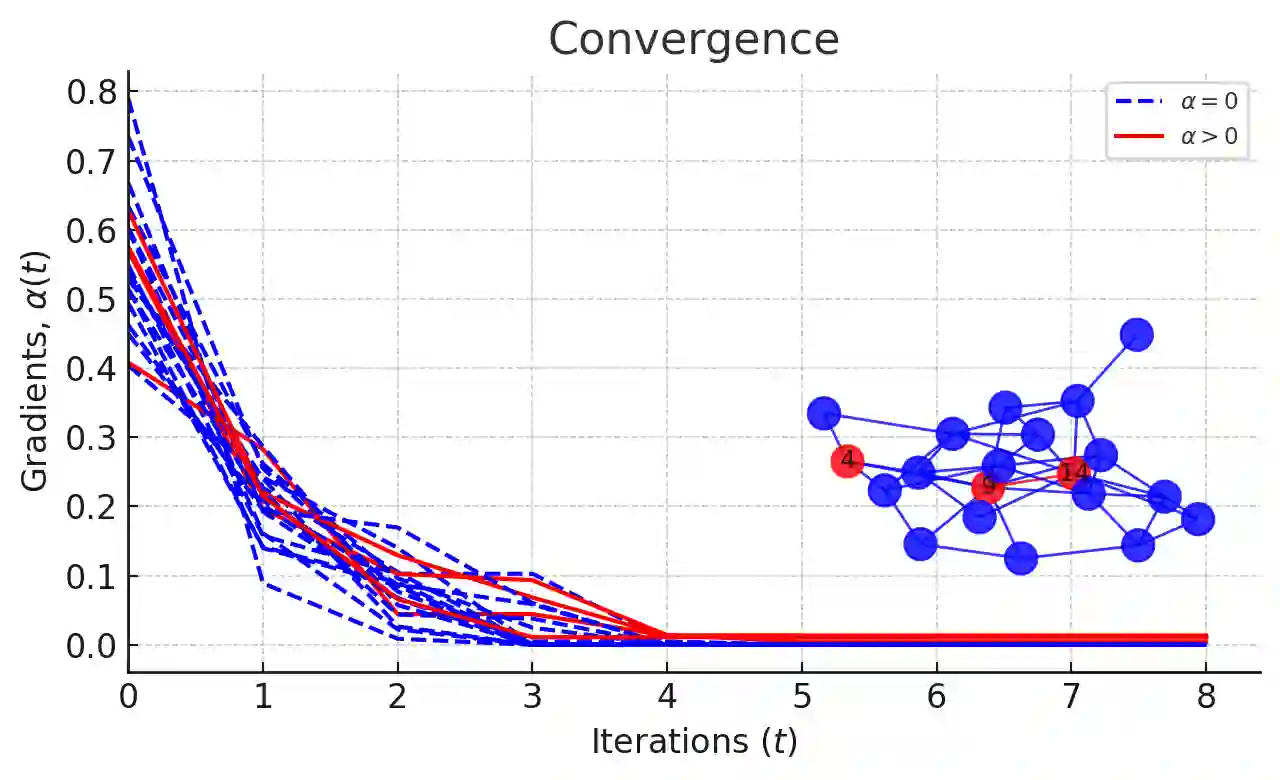
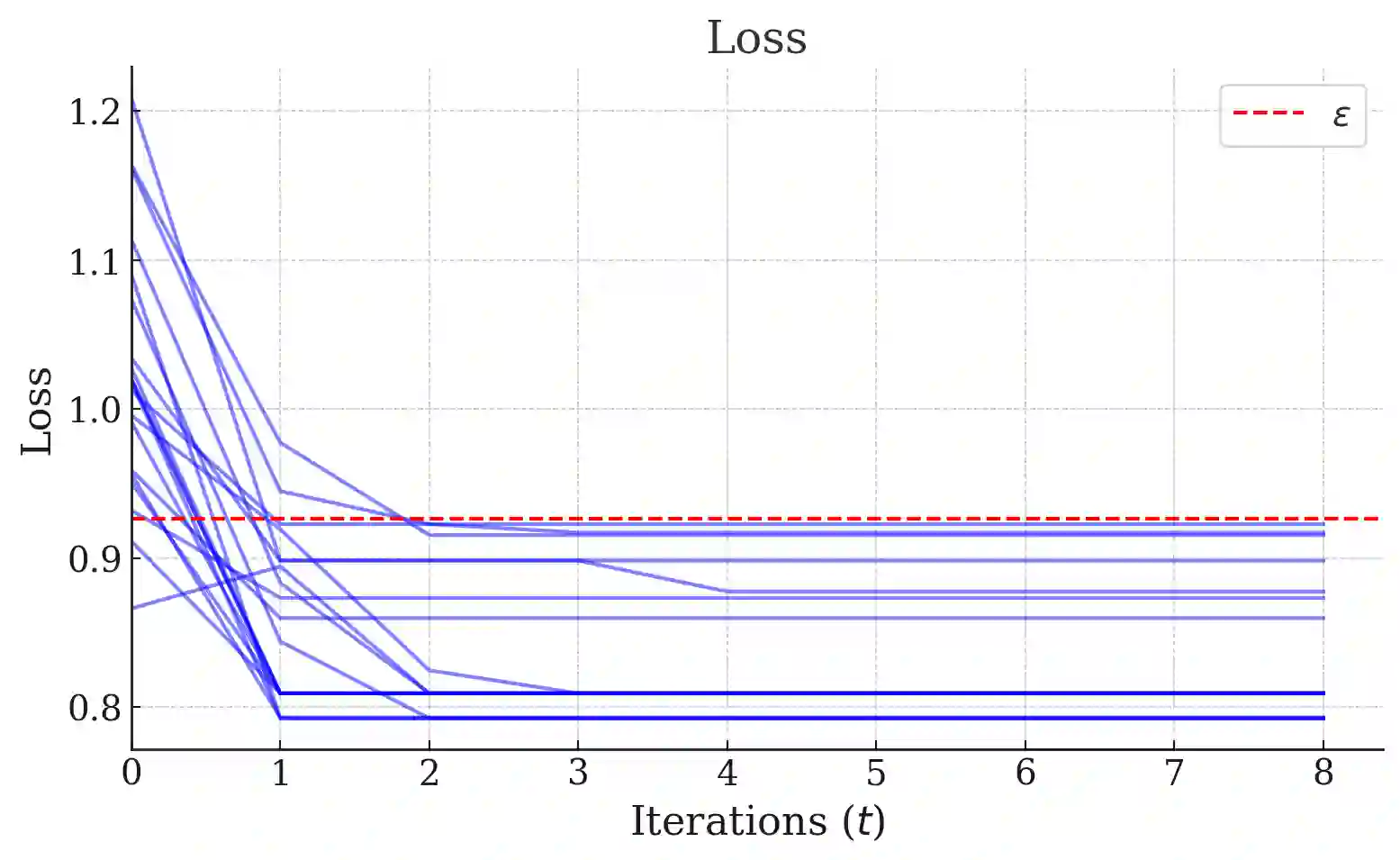
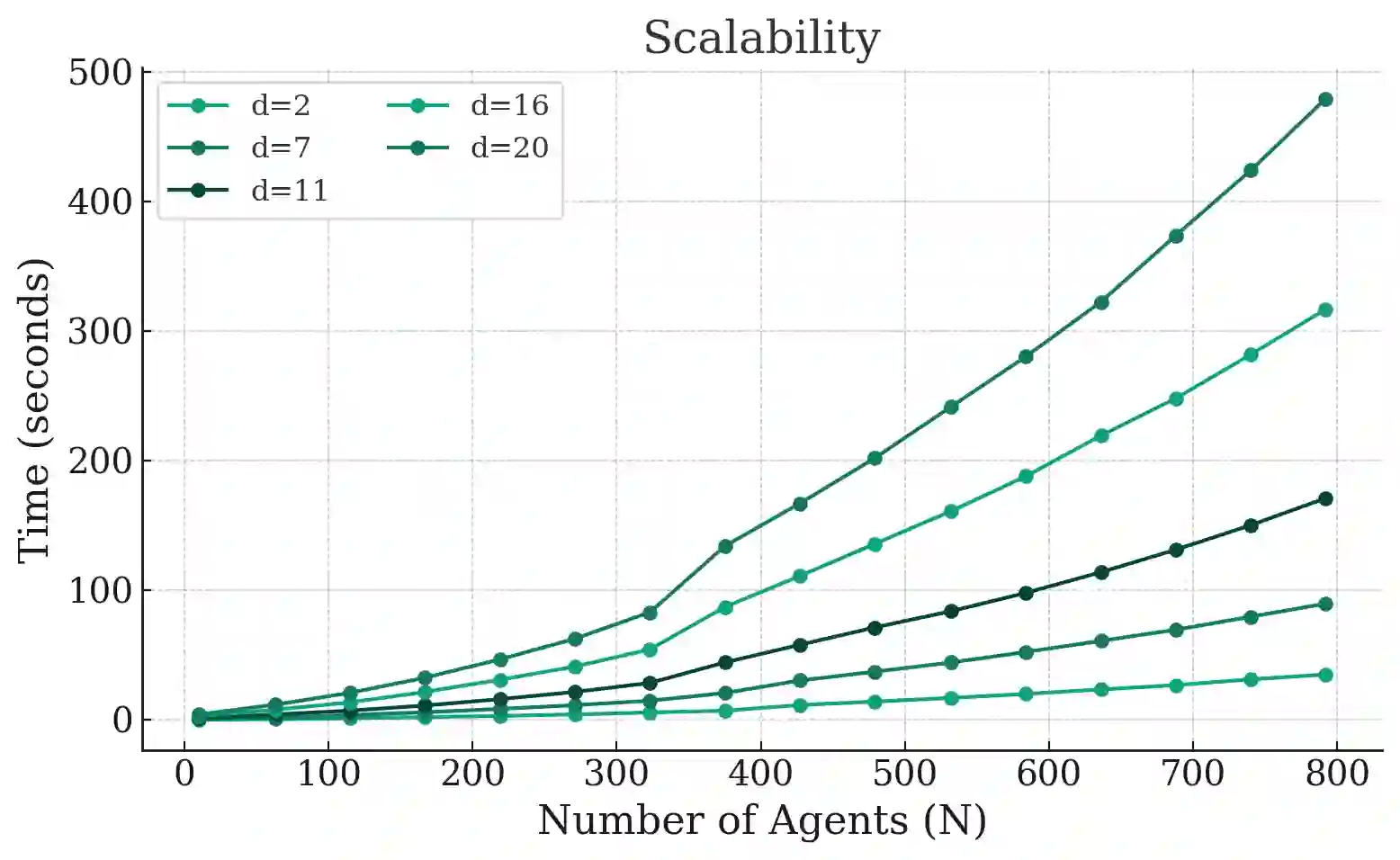
We introduce a decentralized mechanism for pricing and exchanging alternatives constrained by transaction costs. We characterize the time-invariant solutions of a heat equation involving a (weighted) Tarski Laplacian operator, defined for max-plus matrix-weighted graphs, as approximate equilibria of the trading system. We study algebraic properties of the solution sets as well as convergence behavior of the dynamical system. We apply these tools to the "economic problem" of allocating scarce resources among competing uses. Our theory suggests differences in competitive equilibrium, bargaining, or cost-benefit analysis, depending on the context, are largely due to differences in the way that transaction costs are incorporated into the decision-making process. We present numerical simulations of the synchronization algorithm (RRAggU), demonstrating our theoretical findings.
翻译:暂无翻译