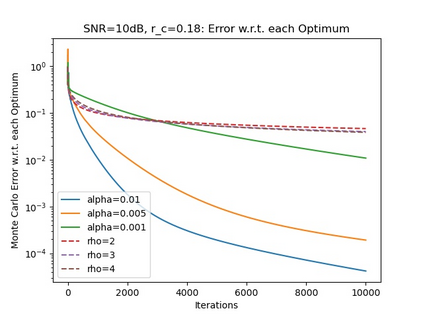
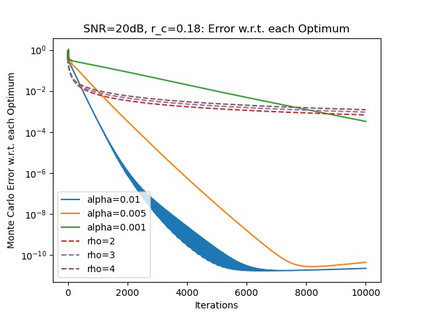
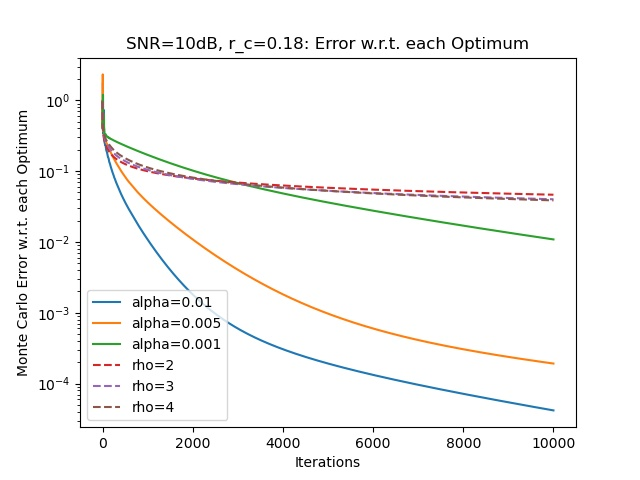
In recent work, we proposed a distributed Banach-Picard iteration (DBPI) that allows a set of agents, linked by a communication network, to find a fixed point of a locally contractive (LC) map that is the average of individual maps held by said agents. In this work, we build upon the DBPI and its local linear convergence (LLC) guarantees to make several contributions. We show that Sanger's algorithm for principal component analysis (PCA) corresponds to the iteration of an LC map that can be written as the average of local maps, each map known to each agent holding a subset of the data. Similarly, we show that a variant of the expectation-maximization (EM) algorithm for parameter estimation from noisy and faulty measurements in a sensor network can be written as the iteration of an LC map that is the average of local maps, each available at just one node. Consequently, via the DBPI, we derive two distributed algorithms - distributed EM and distributed PCA - whose LLC guarantees follow from those that we proved for the DBPI. The verification of the LC condition for EM is challenging, as the underlying operator depends on random samples, thus the LC condition is of probabilistic nature.
翻译:在最近的工作中,我们提出了一个分布式的Banach-Picard复制(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPI)(DBPPI)(DBPPI)(DBPPI)(DPB)(DPPI)(DPI)(DPB)(DPBPI)(DPPPI)(DPLPI)(DBAC)(M)(由通信网络连接起来的每个通讯网点的分布式地图(DBPLC)的分布式地图(LC)(DPAC)(LC)(LC)(LPI)(DPI)(S)(BIPM)(BLC)(BPIPIPIPIPI)(每个地图)的平均数。同样,我们从DBPI(E)中可以证明的地图中找到的地图(EMLC)中找到解算算出两种分布式的地图(LC)的地图(LC), 。