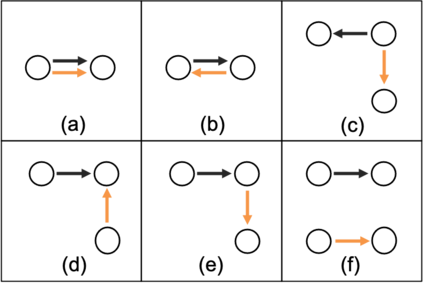
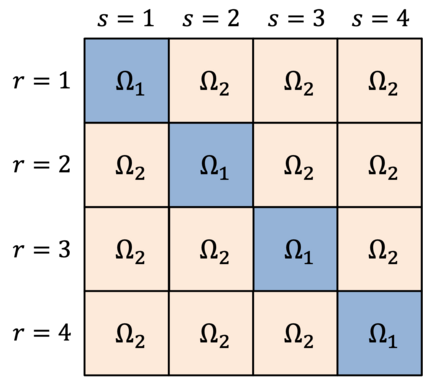
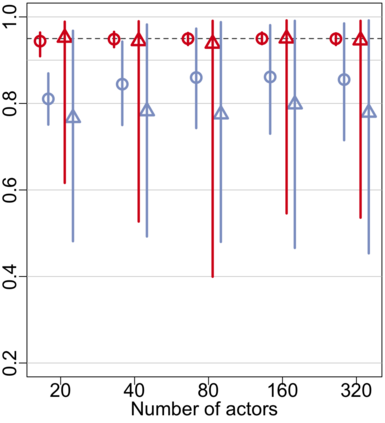
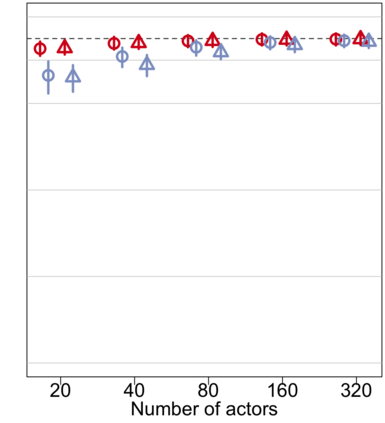
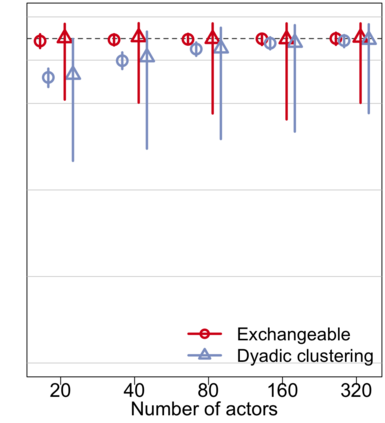
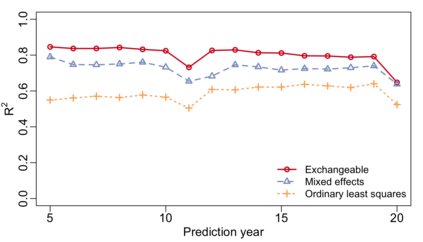
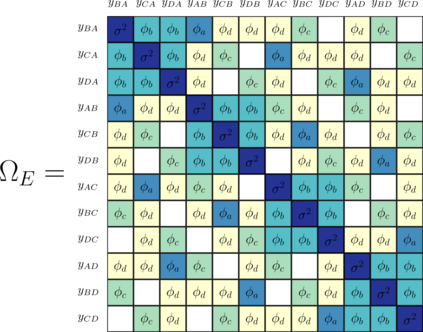
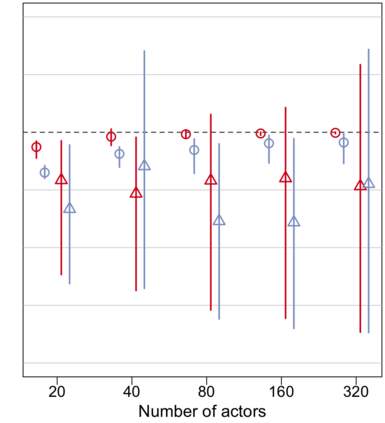
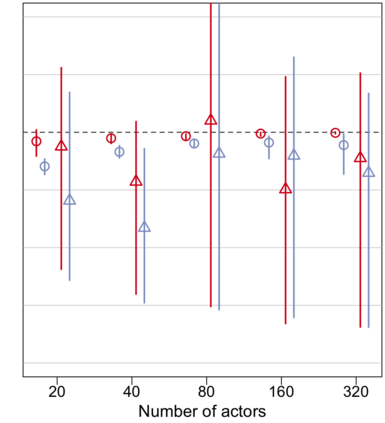
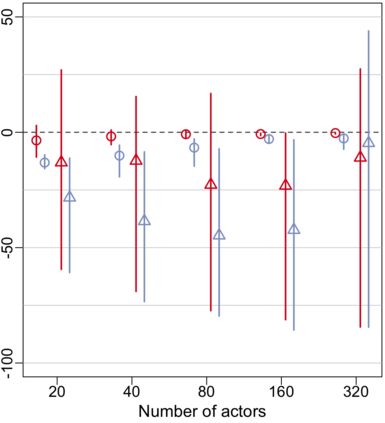
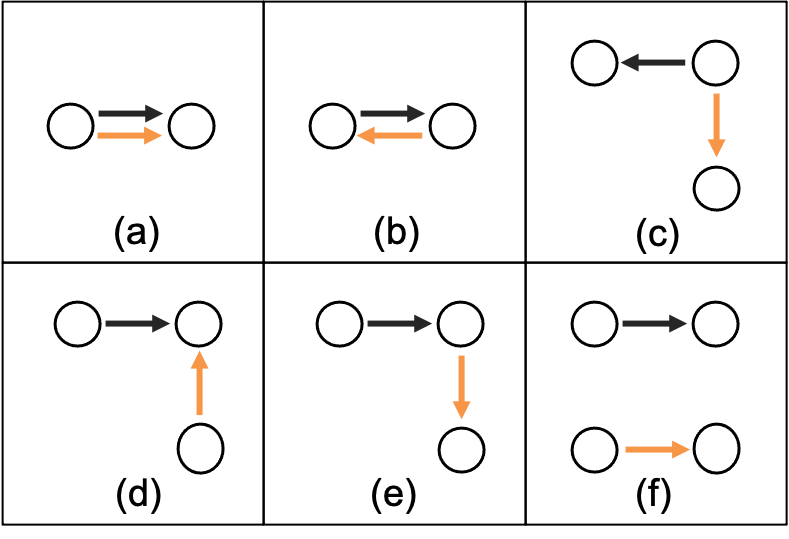
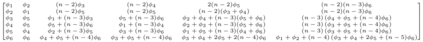Relational arrays represent measures of association between pairs of actors, often in varied contexts or over time. Trade flows between countries, financial transactions between individuals, contact frequencies between school children in classrooms, and dynamic protein-protein interactions are all examples of relational arrays. Elements of a relational array are often modeled as a linear function of observable covariates. Uncertainty estimates for regression coefficient estimators -- and ideally the coefficient estimators themselves -- must account for dependence between elements of the array (e.g. relations involving the same actor) and existing estimators of standard errors that recognize such relational dependence rely on estimating extremely complex, heterogeneous structure across actors. This paper develops a new class of parsimonious coefficient and standard error estimators for regressions of relational arrays. We leverage an exchangeability assumption to derive standard error estimators that pool information across actors and are substantially more accurate than existing estimators in a variety of settings. This exchangeability assumption is pervasive in network and array models in the statistics literature, but not previously considered when adjusting for dependence in a regression setting with relational data. We demonstrate improvements in inference theoretically, via a simulation study, and by analysis of a data set involving international trade.
翻译:关系阵列的元素往往以可观察到的共变数的线性函数为模型,对回归系数估计值的不确定性估计值 -- -- 理想的系数本身 -- -- 必须说明阵列各要素(例如涉及同一行为者的关系)和现有估计值之间的依赖性。这种交换性假设在统计文献的网络和阵列模型中很普遍,但在调整回归依赖性时,我们通过模拟数据,通过模拟数据,通过模拟分析,我们用一套数据显示改进。