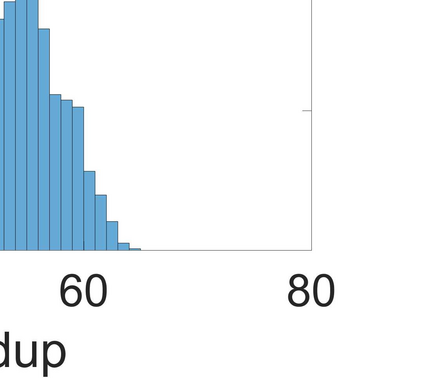
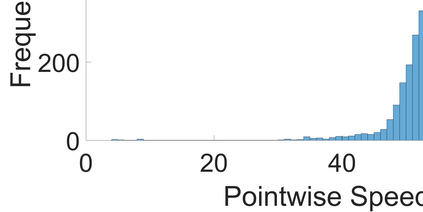
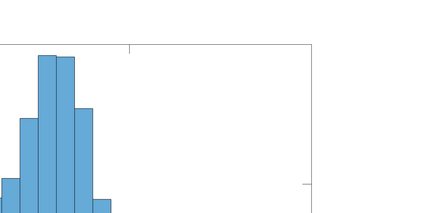
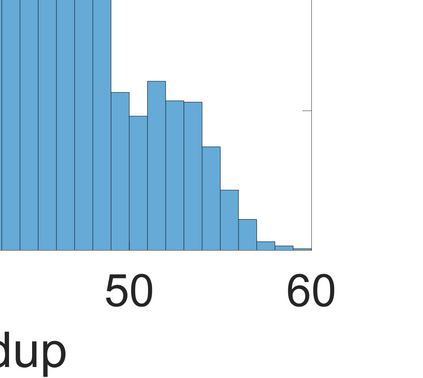
Uncertainty in physical parameters can make the solution of forward or inverse light scattering problems in astrophysical, biological, and atmospheric sensing applications, cost prohibitive for real-time applications. For example, given a probability density in the parametric space of dimensions, refractive index and wavelength, the number of required evaluations for the expected scattering increases dramatically. In the case of dielectric and weakly absorbing spherical particles (both homogeneous and layered), we begin with a Fraunhofer approximation of the scattering coefficients consisting of Riccati-Bessel functions, and reduce it into simpler nested trigonometric approximations. They provide further computational advantages when parameterized on lines of constant optical path lengths. This can reduce the cost of evaluations by large factors $\approx$ 50, without a loss of accuracy in the integrals of these scattering coefficients. We analyze the errors of the proposed approximation, and present numerical results for a set of forward problems as a demonstration.
翻译:物理参数的不确定性可以使天体物理、生物和大气遥感应用中的前向或反向散射问题得到解决,而实时应用的成本却令人望而却步。例如,鉴于尺寸的参数空间的概率密度、折射指数和波长,对预期散射所需的评价数量急剧增加。在电离和微弱吸收球状颗粒(同质和分层)的情况下,我们首先从由Riccati-Bessel函数组成的散射系数的Fraunhofer近似法开始,将其降低为更简单的嵌套三角近似法。当以恒定光路长度线为参数时,它们提供了进一步的计算优势。这可以大大降低评价成本,但不会丧失这些散射系数的精度。我们分析了拟议的近似值的错误,并提出了一系列远期问题的数字结果作为示范。