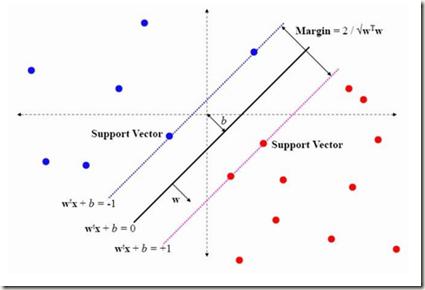
We show how, using linear-algebraic tools developed to prove Tverberg's theorem in combinatorial geometry, we can design new models of multi-class support vector machines (SVMs). These supervised learning protocols require fewer conditions to classify sets of points, and can be computed using existing binary SVM algorithms in higher-dimensional spaces, including soft-margin SVM algorithms. We describe how the theoretical guarantees of standard support vector machines transfer to these new classes of multi-class support vector machines. We give a new simple proof of a geometric characterization of support vectors for largest margin SVMs by Veelaert.
翻译:暂无翻译
相关内容
专知会员服务
34+阅读 · 2020年1月15日
专知会员服务
34+阅读 · 2019年10月18日
专知会员服务
36+阅读 · 2019年10月17日
InteractE: Improving Convolution-based Knowledge Graph Embeddings by Increasing Feature Interactions
Arxiv
13+阅读 · 2019年11月1日
Arxiv
13+阅读 · 2018年1月18日