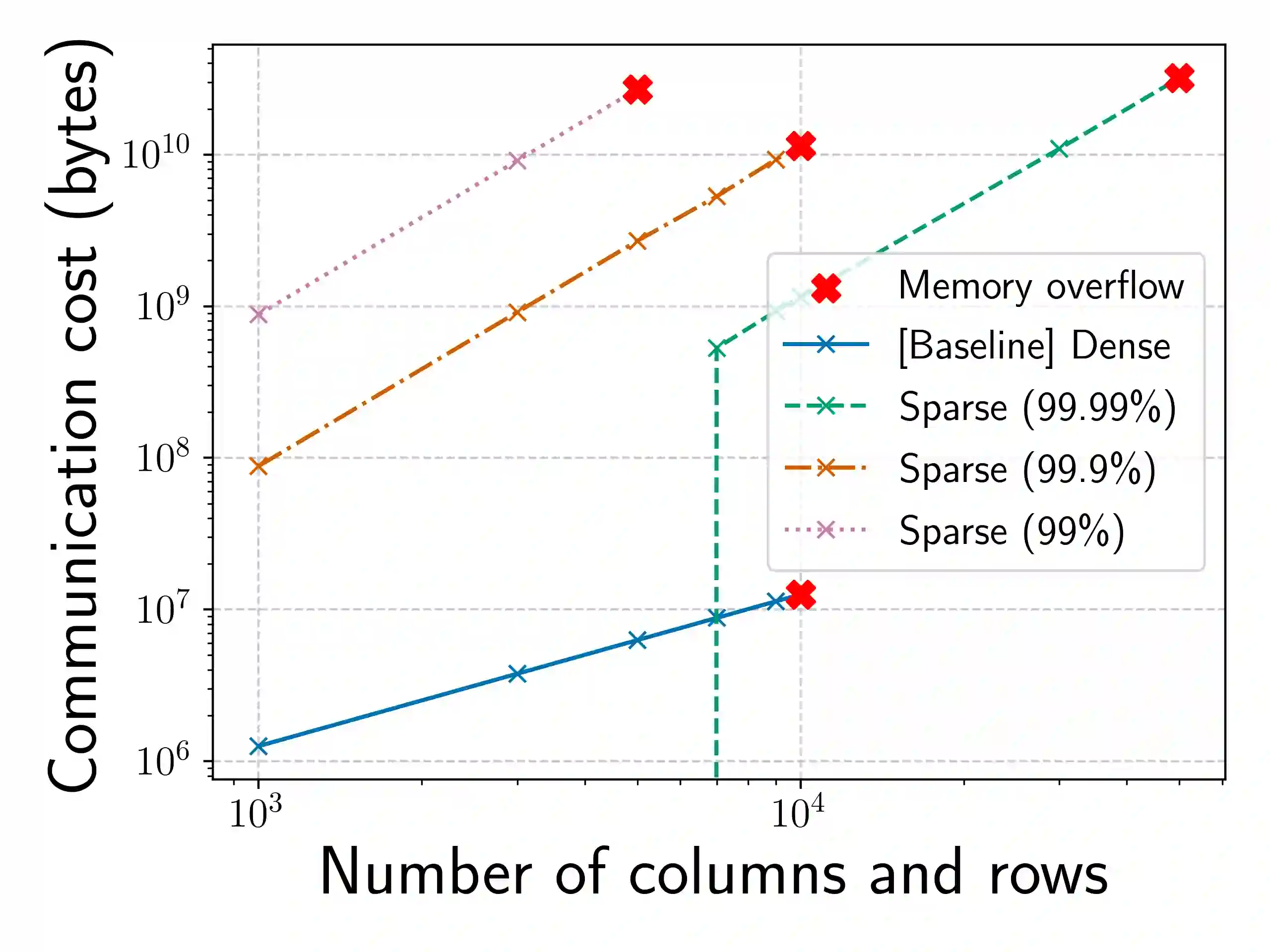
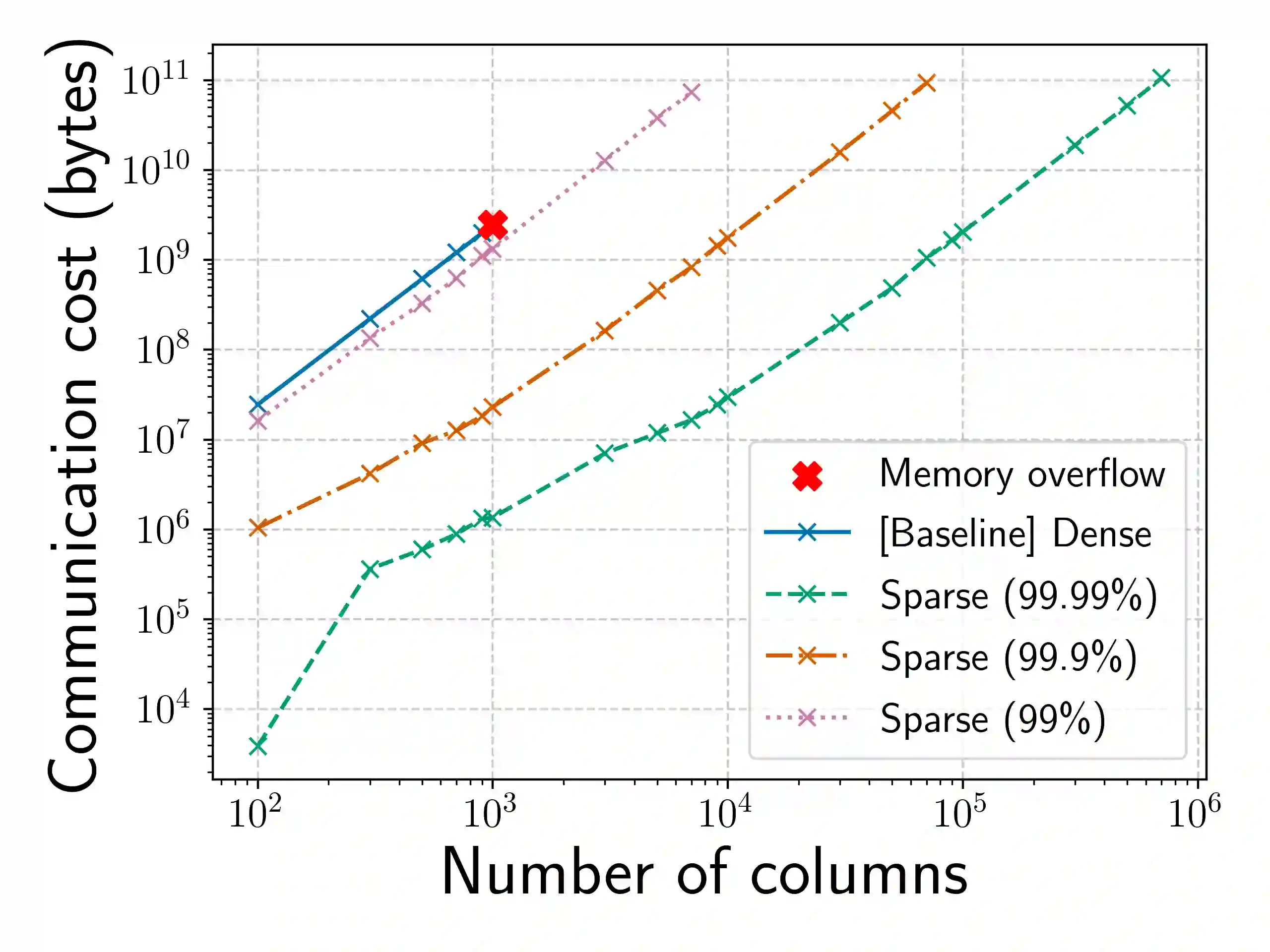
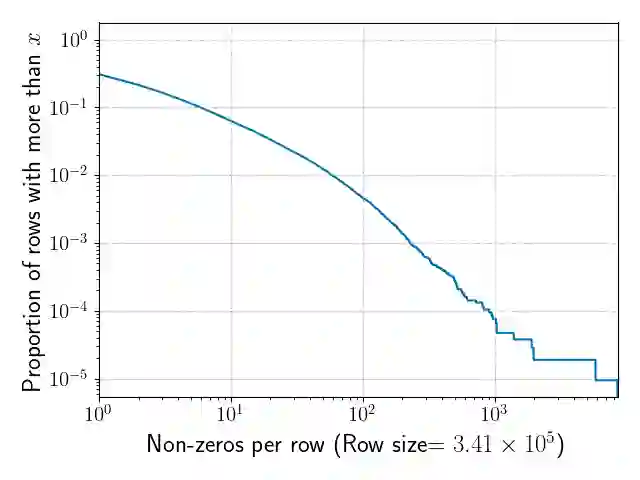
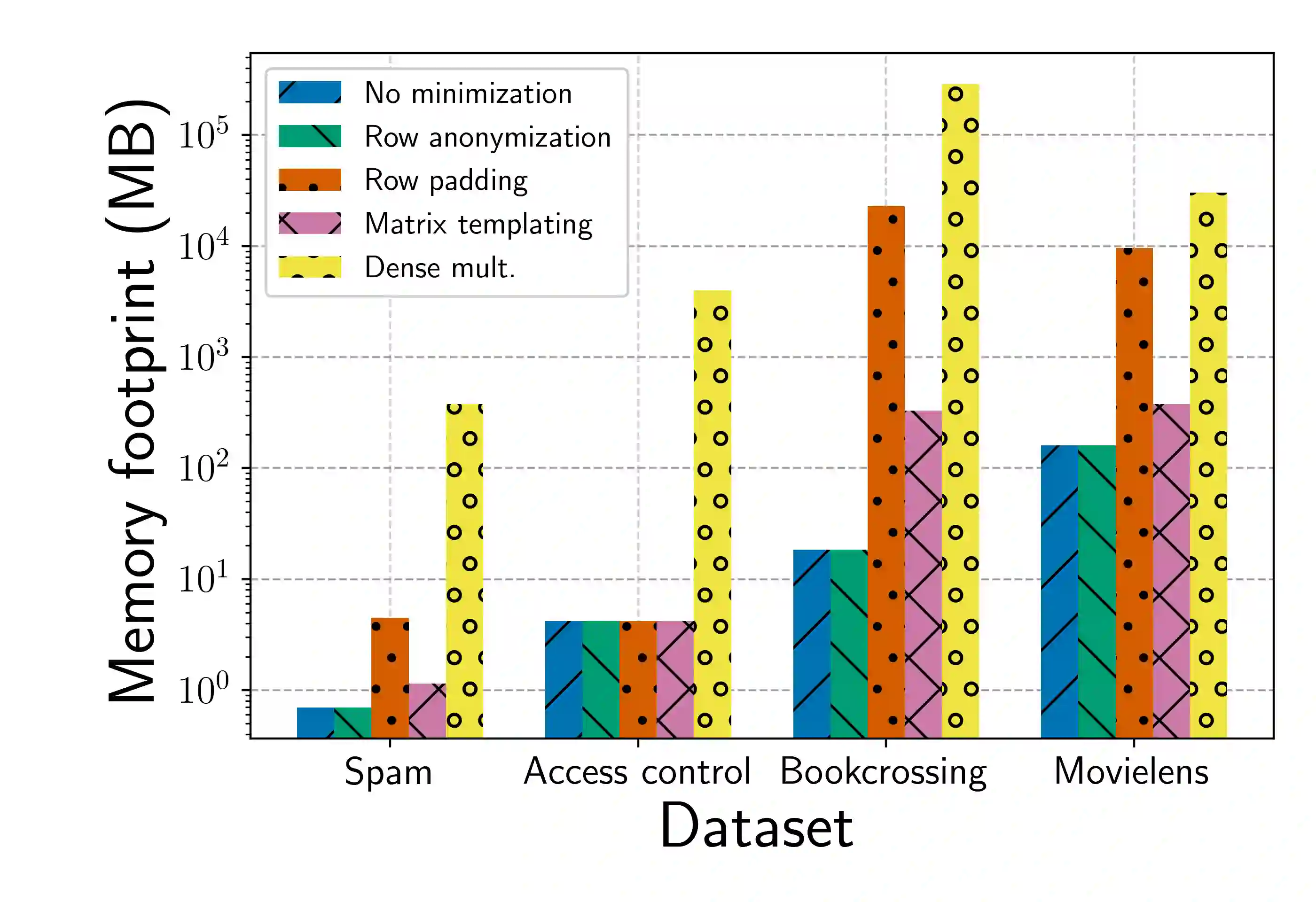
To preserve privacy, multi-party computation (MPC) enables executing Machine Learning (ML) algorithms on secret-shared or encrypted data. However, existing MPC frameworks are not optimized for sparse data. This makes them unsuitable for ML applications involving sparse data, e.g., recommender systems or genomics. Even in plaintext, such applications involve high-dimensional sparse data, that cannot be processed without sparsity-related optimizations due to prohibitively large memory requirements. Since matrix multiplication is central in ML algorithms, we propose MPC algorithms to multiply secret sparse matrices. On the one hand, our algorithms avoid the memory issues of the "dense" data representation of classic secure matrix multiplication algorithms. On the other hand, our algorithms can significantly reduce communication costs (some experiments show a factor 1000) for realistic problem sizes. We validate our algorithms in two ML applications in which existing protocols are impractical. An important question when developing MPC algorithms is what assumptions can be made. In our case, if the number of non-zeros in a row is a sensitive piece of information then a short runtime may reveal that the number of non-zeros is small. Existing approaches make relatively simple assumptions, e.g., that there is a universal upper bound to the number of non-zeros in a row. This often doesn't align with statistical reality, in a lot of sparse datasets the amount of data per instance satisfies a power law. We propose an approach which allows adopting a safe upper bound on the distribution of non-zeros in rows/columns of sparse matrices.
翻译:暂无翻译