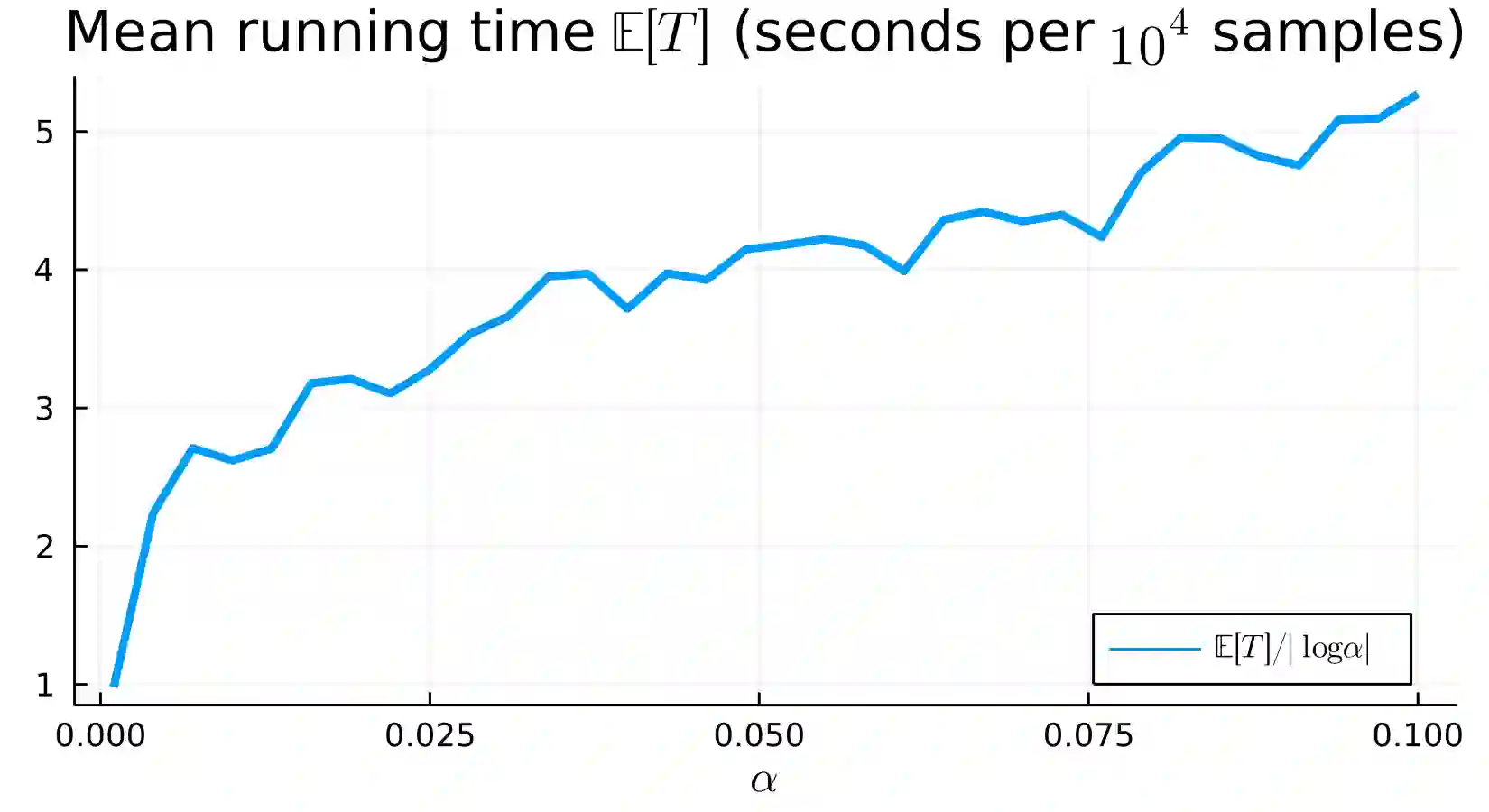
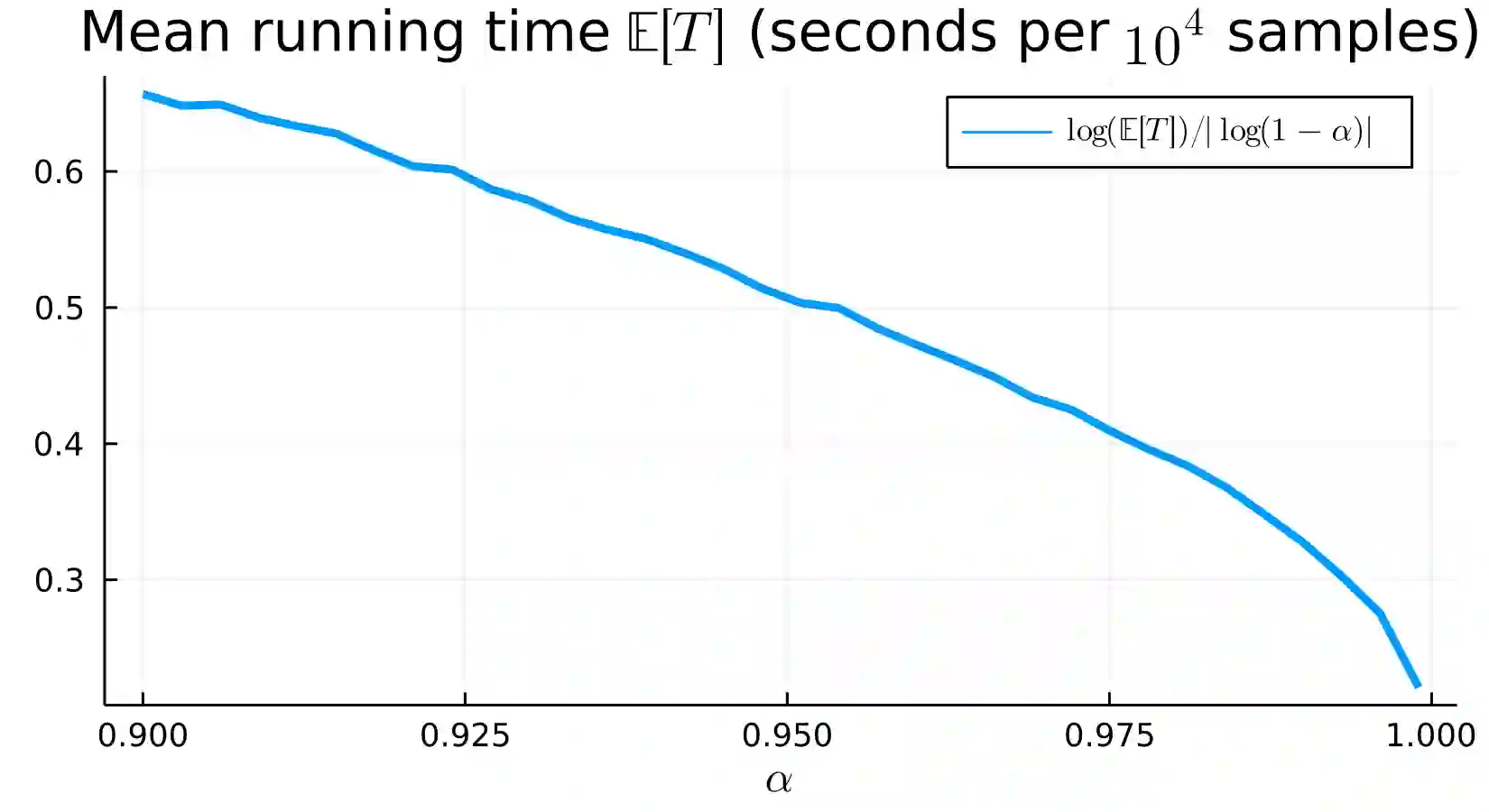
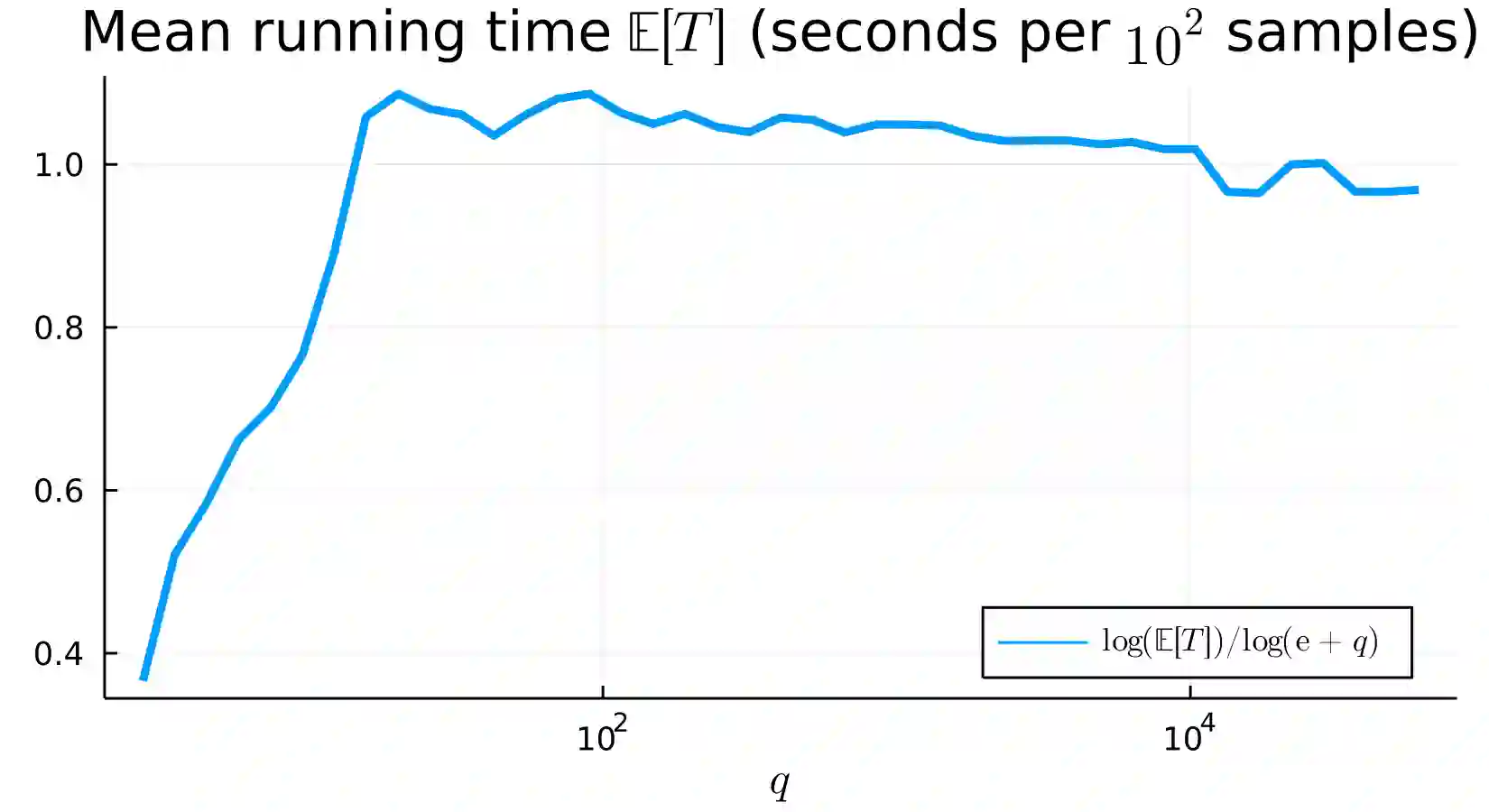
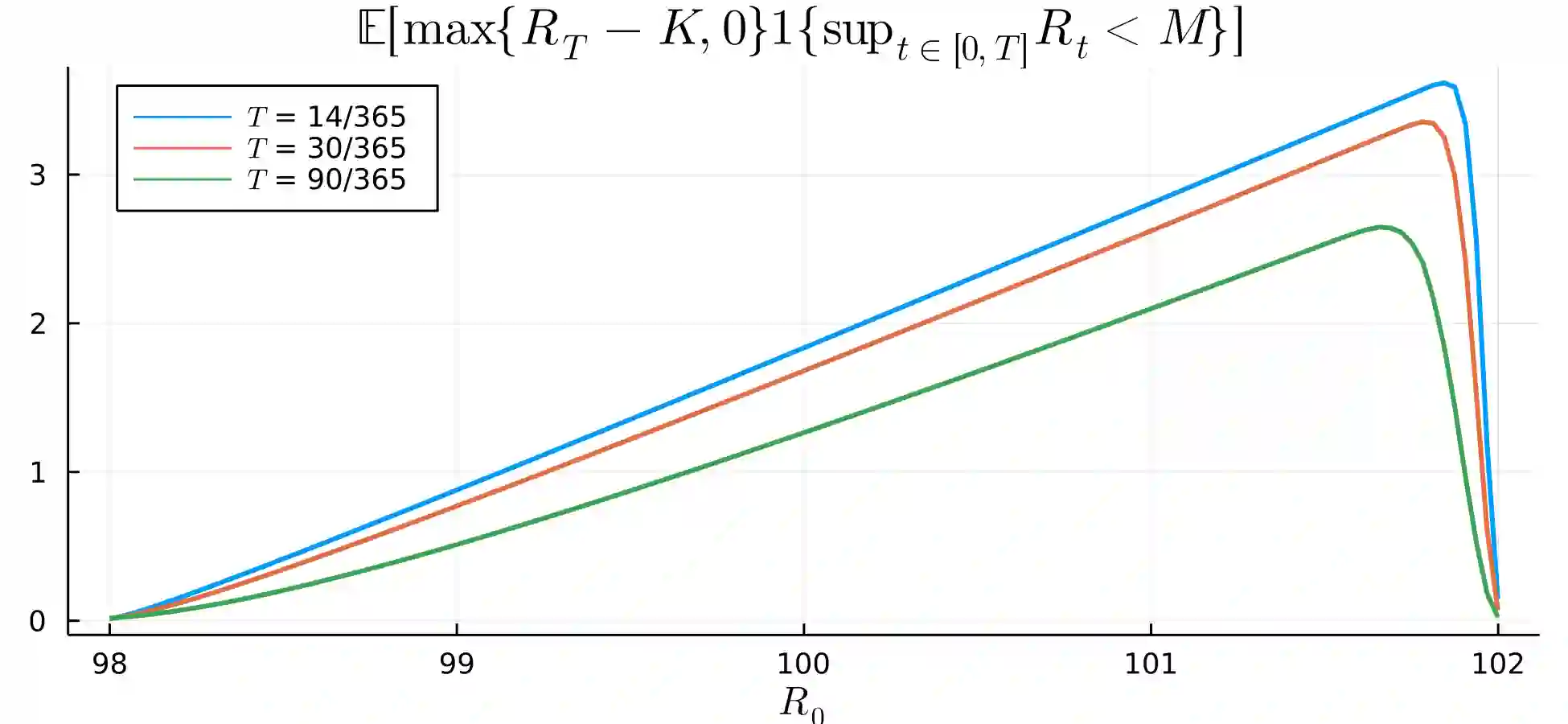
We construct a fast exact algorithm for the simulation of the first-passage time, jointly with the undershoot and overshoot, of a tempered stable subordinator over an arbitrary non-increasing absolutely continuous function. We prove that the running time of our algorithm has finite exponential moments and provide bounds on its expected running time with explicit dependence on the characteristics of the process and the initial value of the function. The expected running time grows at most cubically in the stability parameter (as it approaches either $0$ or $1$) and is linear in the tempering parameter and the initial value of the function. Numerical performance, based on the implementation in the dedicated GitHub repository, exhibits a good agreement with our theoretical bounds. We provide numerical examples to illustrate the performance of our algorithm in Monte Carlo estimation.
翻译:我们构建了一个快速准确的算法,用于模拟温和稳定子进程在任意非下降绝对连续函数上的第一遍历时间,以及下限和上限。我们证明了我们的算法的运行时间具有有限的指数矩,并提供了对其预期运行时间的界限,其中明确地涉及到了过程的特征和函数的初始值。预期运行时间在稳定参数(当稳定参数趋近0或1时)以至多三次方增长,并且在调节参数和函数的初始值方面是线性的。根据专用的GitHub存储库中的实现的数值表现,我们提供了数值例子来说明我们的算法在蒙特卡罗估计中的性能。