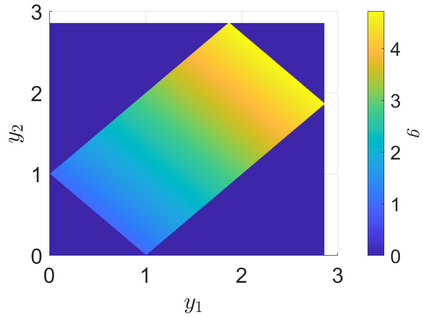
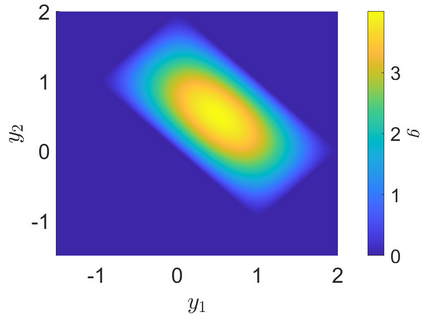
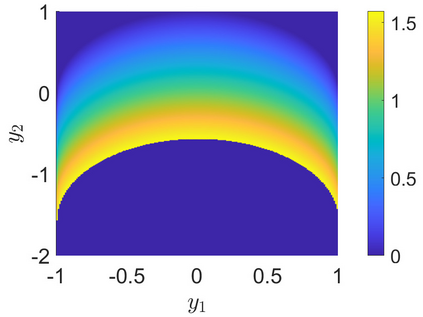
We consider the numerical solution of the optimal transport problem between densities that are supported on sets of unequal dimension. Recent work by McCann and Pass reformulates this problem into a non-local Monge-Amp\`ere type equation. We provide a new level set framework for interpreting this non-linear PDE. We also propose a novel discretisation that combines carefully constructed monotone finite difference schemes with a variable-support discrete version of the Dirac delta function. The resulting method is consistent and monotone. These new techniques are described and implemented in the setting of 1D to 2D transport, but can easily be generalised to higher dimensions. Several challenging computational tests validate the new numerical method.
翻译:暂无翻译