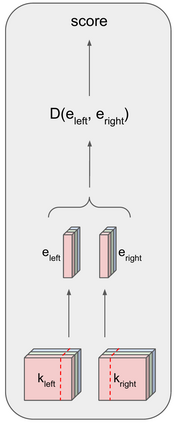
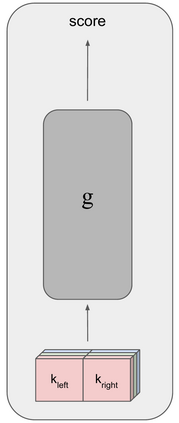
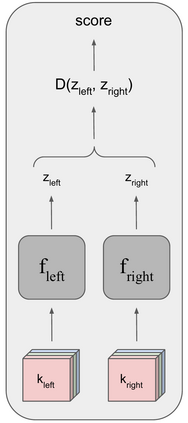
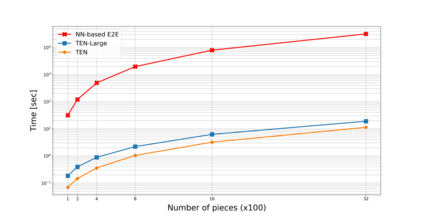
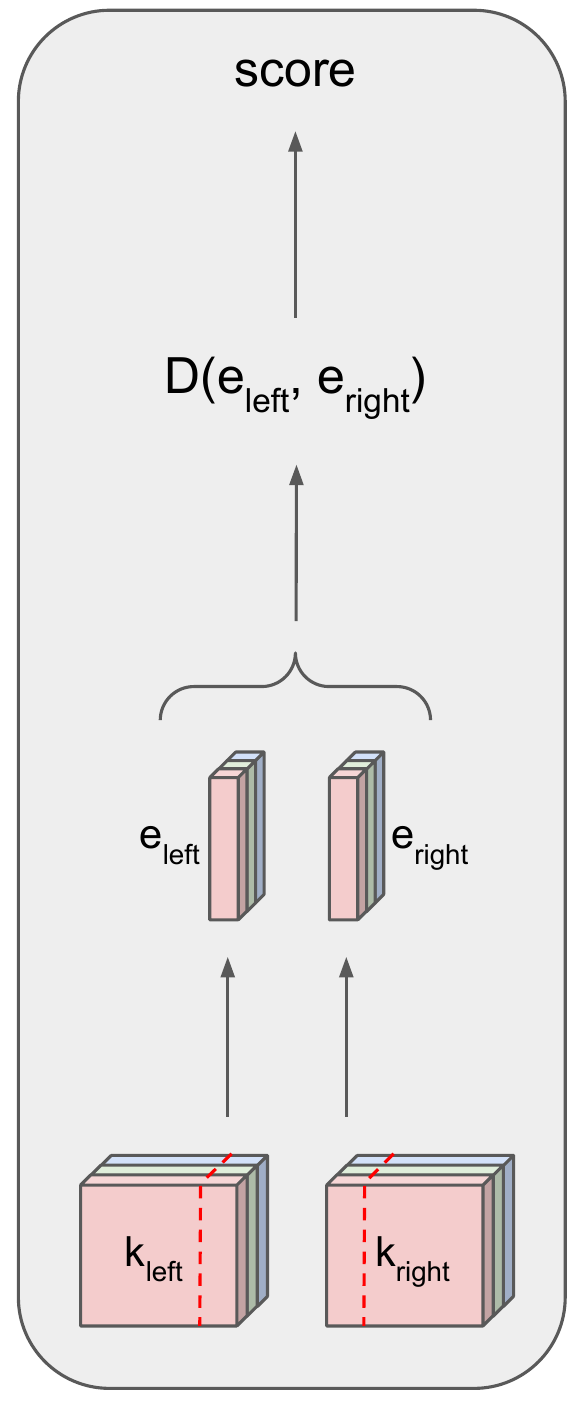
This paper introduces the novel CNN-based encoder Twin Embedding Network (TEN), for the jigsaw puzzle problem (JPP), which represents a puzzle piece with respect to its boundary in a latent embedding space. Combining this latent representation with a simple distance measure, we demonstrate improved accuracy levels of our newly proposed pairwise compatibility measure (CM), compared to that of various classical methods, for degraded puzzles with eroded tile boundaries. We focus on this problem instance for our case study, as it serves as an appropriate testbed for real-world scenarios. Specifically, we demonstrated an improvement of up to 8.5% and 16.8% in reconstruction accuracy, for so-called Type-1 and Type-2 problem variants, respectively. Furthermore, we also demonstrated that TEN is faster by a few orders of magnitude, on average, than a typical deep neural network (NN) model, i.e., it is as fast as the classical methods. In this regard, the paper makes a significant first attempt at bridging the gap between the relatively low accuracy (of classical methods and the intensive computational complexity (of NN models), for practical, real-world puzzle-like problems.
翻译:本文介绍了新颖的CNN编码器双嵌入网络(TEN), 用于拼图拼图问题(JPP), 它代表了在潜伏的嵌入空间中其边界的一个谜题。 将这种潜在代表与简单的距离测量相结合, 我们展示了我们新提议的双向兼容度测量(CM)的精确度, 与各种经典方法相比, 与被侵蚀的瓷砖边界的退化拼图相比, 更加精确。 我们的案例研究侧重于这个问题, 因为它是真实世界情景的适当测试。 具体地说, 在重建精度方面, 我们展示了高达8.5%和16.8%的精确度, 分别是所谓的类型1和类型2问题变异体。 此外, 我们还表明,对于实际的、 现实世界的谜题来说, TEN 比典型的深层网络模型(NNN) 速度要快, 也就是说, 它与经典方法一样快。 在这方面, 文件首次尝试弥合相对低的精确度( 经典方法) 和密集的计算复杂度( NNN模型) 之间的差距。