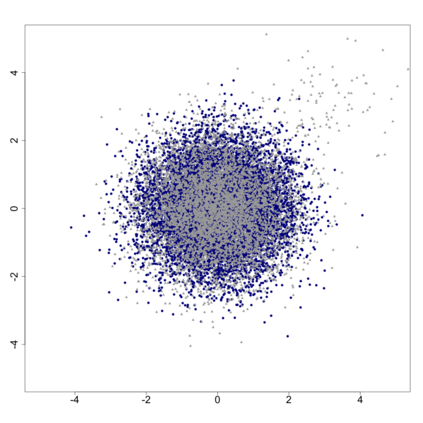
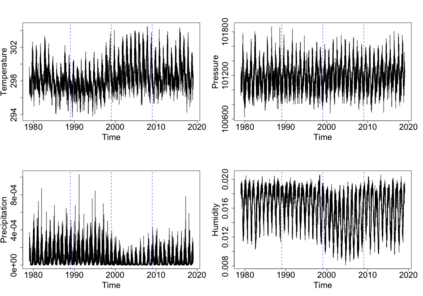
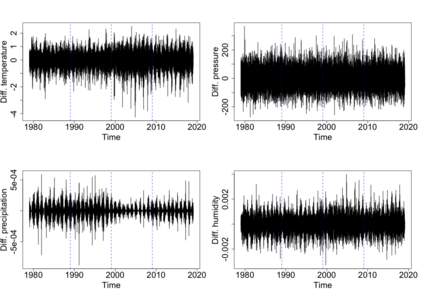
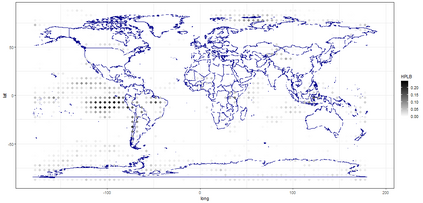
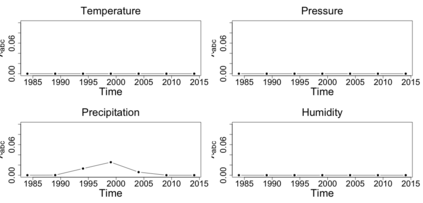
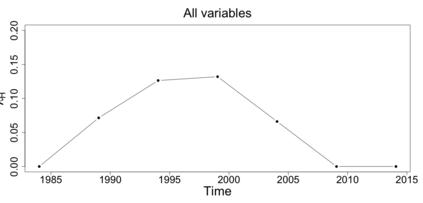
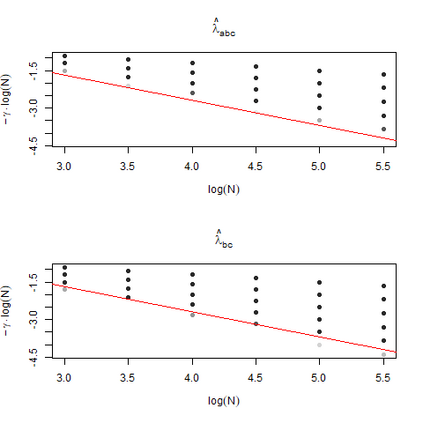
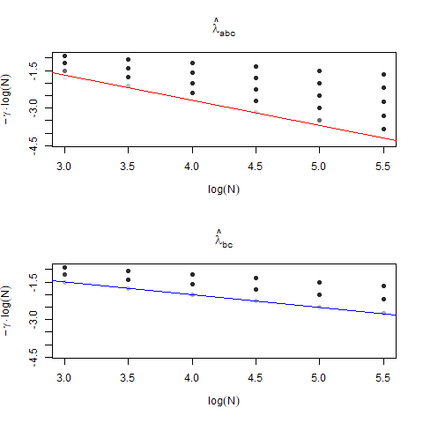
The statistics and machine learning communities have recently seen a growing interest in classification-based approaches to two-sample testing. The outcome of a classification-based two-sample test remains a rejection decision, which is not always informative since the null hypothesis is seldom strictly true. Therefore, when a test rejects, it would be beneficial to provide an additional quantity serving as a refined measure of distributional difference. In this work, we introduce a framework for the construction of high-probability lower bounds on the total variation distance. These bounds are based on a one-dimensional projection, such as a classification or regression method, and can be interpreted as the minimal fraction of samples pointing towards a distributional difference. We further derive asymptotic power and detection rates of two proposed estimators and discuss potential uses through an application to a reanalysis climate dataset.
翻译:最近,统计和机器学习界对基于分类的两样测试方法的兴趣日益浓厚,基于分类的两样测试的结果仍然是拒绝决定,由于无效假设很少严格无误,这种拒绝并非总能提供信息,因此,在试验拒绝时,最好提供额外数量,作为改善分布差异的衡量标准。在这项工作中,我们引入了一个框架,用于构建关于全变差距离的高概率下限,这些界限以一维预测为基础,如分类或回归法,可以被解释为指向分布差异的样本的最小比例。我们进一步得出两个拟议估计值的零反应力和检测率,并通过对气候数据集进行再分析来讨论潜在用途。