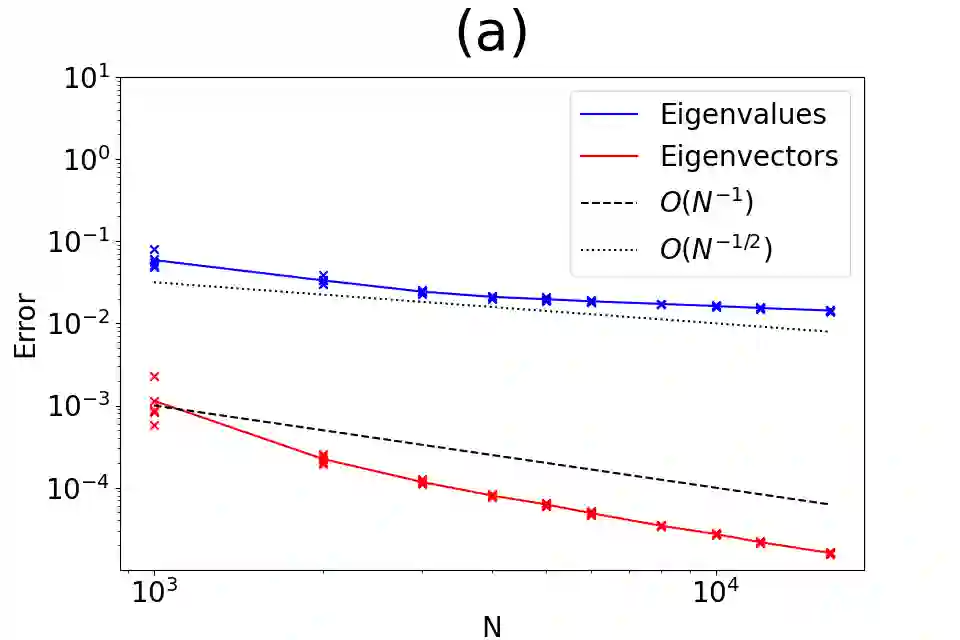
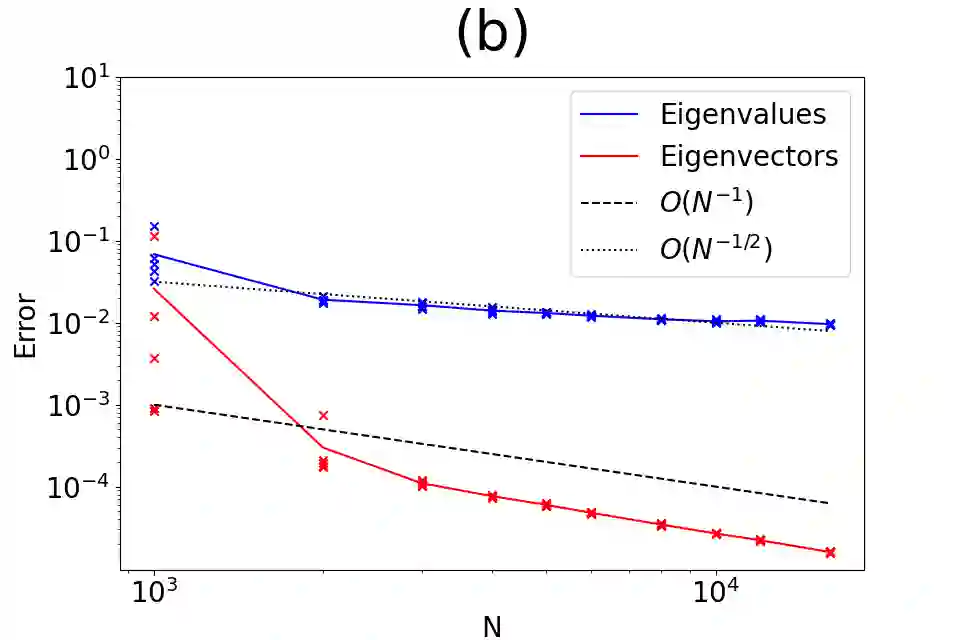
In this work, we introduce a numerical method for approximating arbitrary differential operators on vector fields in the weak form given point cloud data sampled randomly from a $d$ dimensional manifold embedded in $\mathbb{R}^n$. This method generalizes the local linear mesh method to the local curved mesh method, thus, allowing for the estimation of differential operators with nontrivial Christoffer symbols, such as the Bochner or Hodge Laplacians. In particular, we leverage the potentially small intrinsic dimension of the manifold $(d \ll n)$ to construct local parameterizations that incorporate both local meshes and higher-order curvature information. The former is constructed using low dimensional meshes obtained from local data projected to the tangent spaces, while the latter is obtained by fitting local polynomials with the generalized moving least squares. Theoretically, we prove the weak and spectral convergence rates for the proposed method for the estimation of the Bochner Laplacian. We provide numerical results supporting the theoretical convergence rates for the Bochner and Hodge Laplacians on simple manifolds.
翻译:暂无翻译