Exponential time propagators for elastodynamics

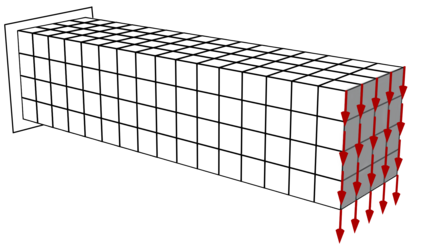
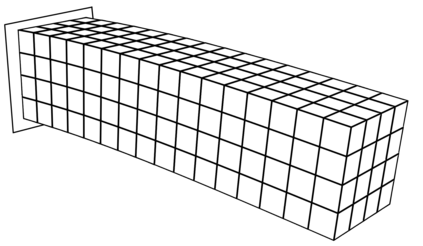
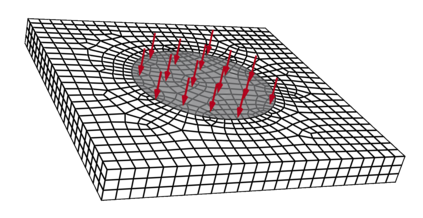
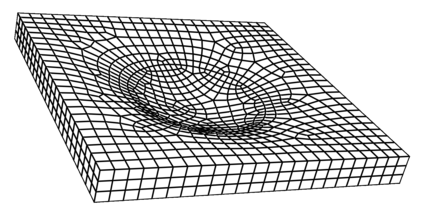
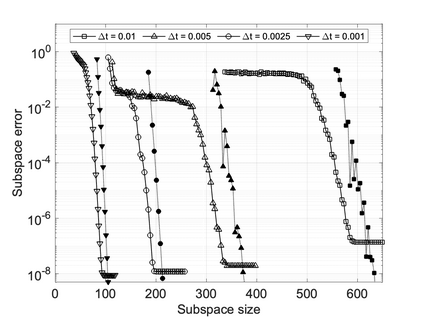
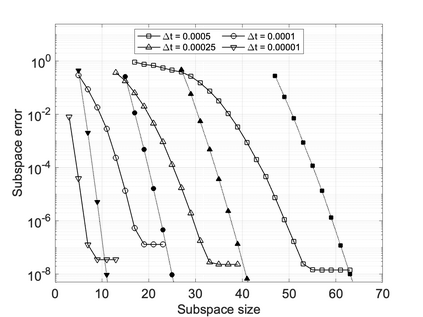
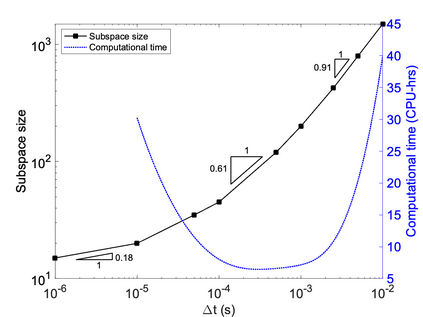
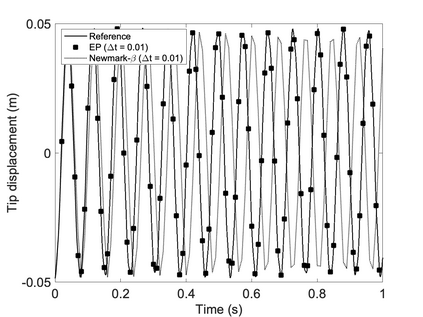
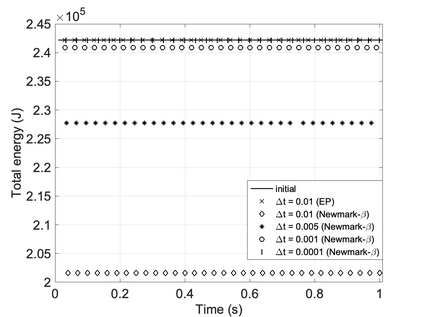
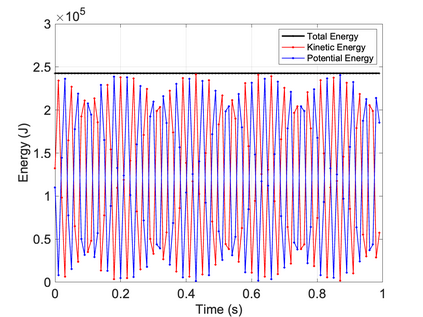
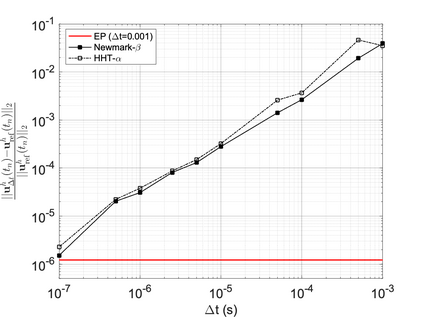
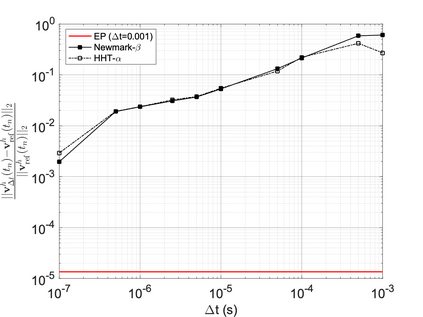
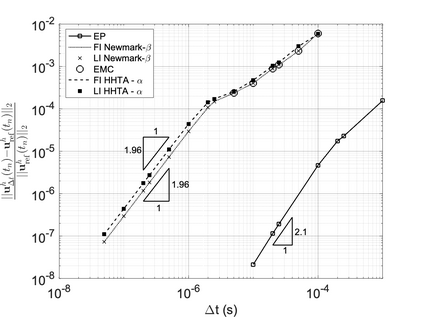
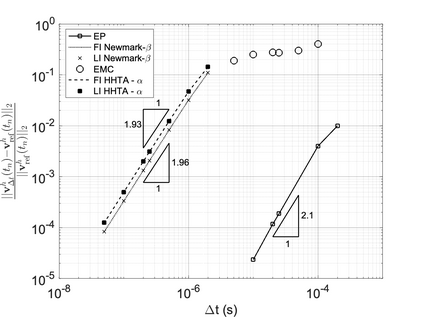
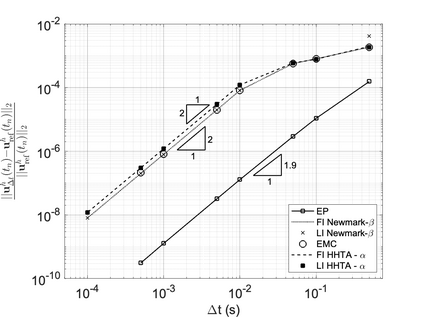
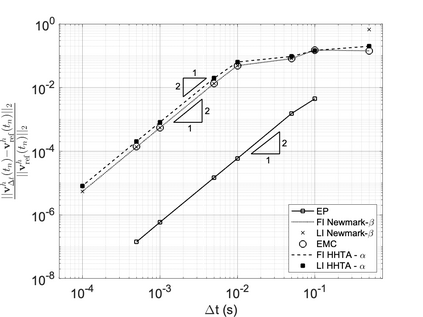
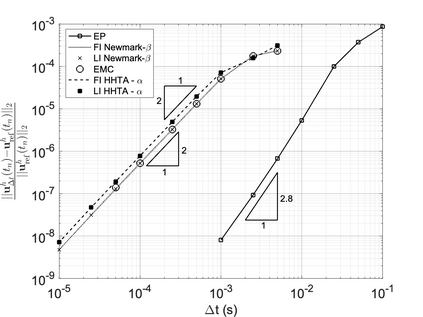
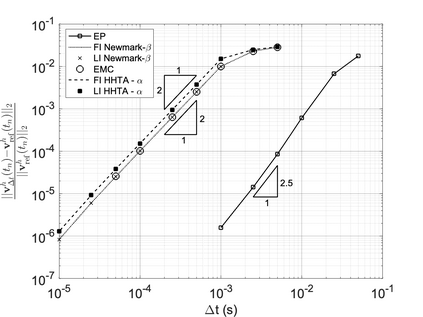
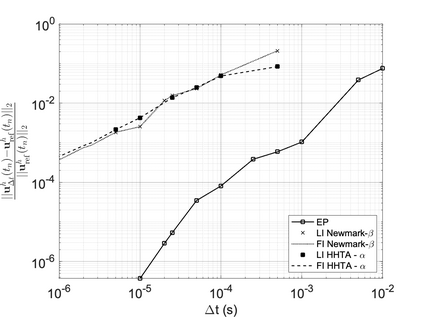
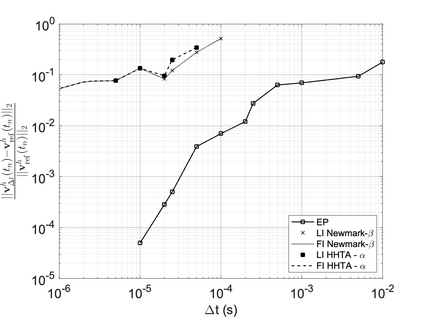
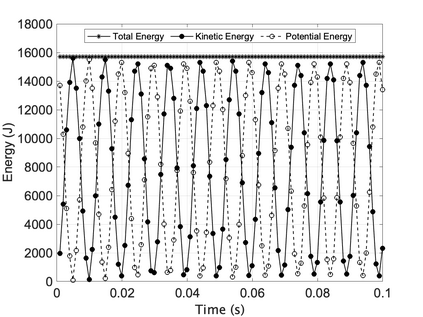
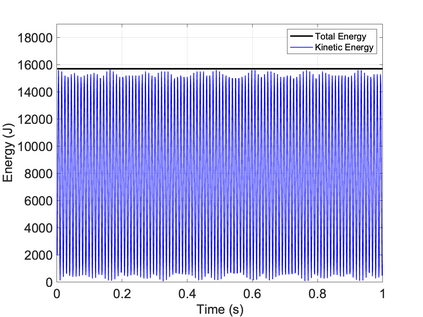
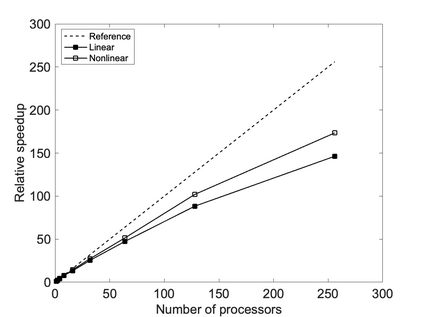
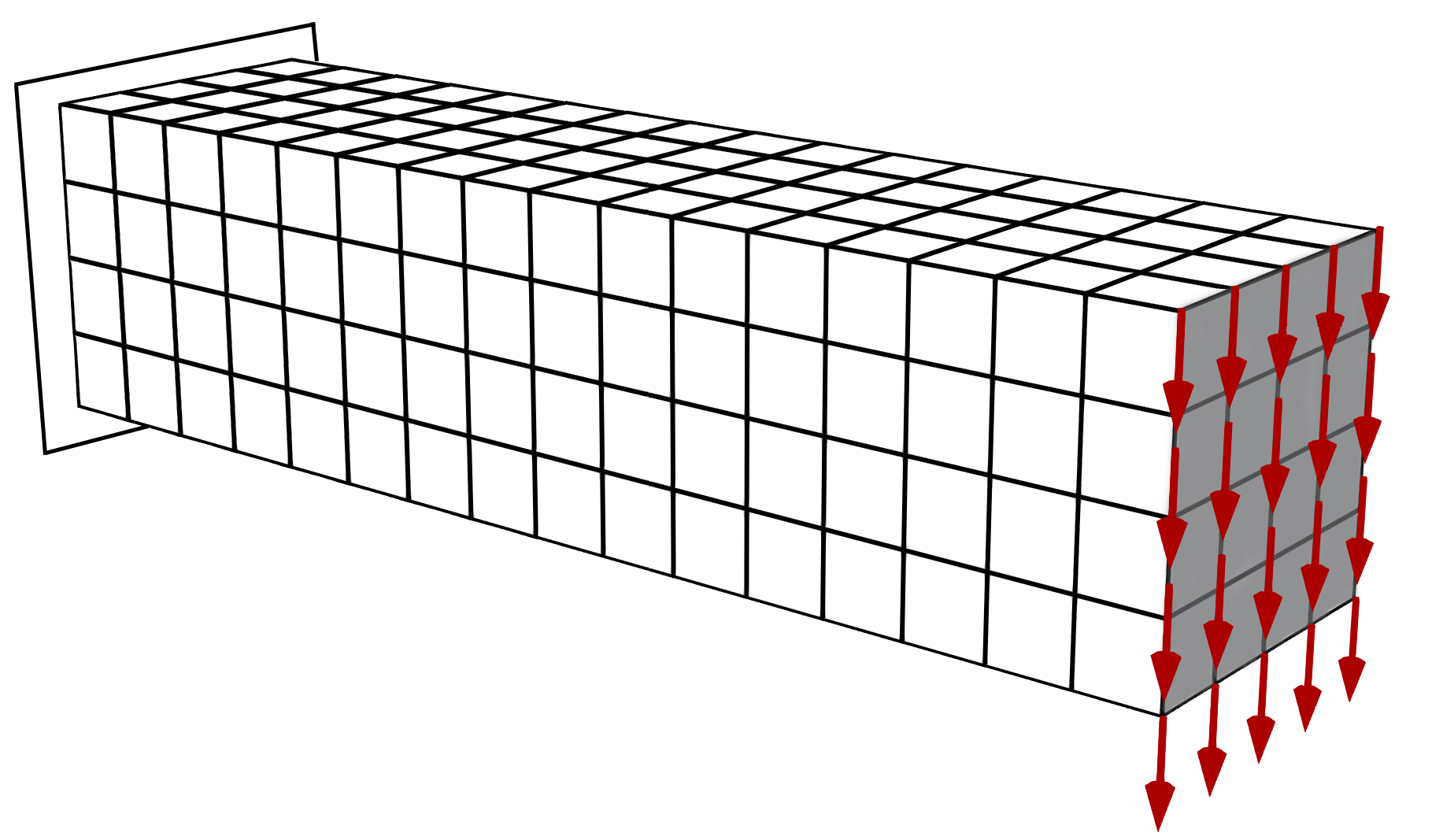
We propose a computationally efficient and systematically convergent approach for elastodynamics simulations. We recast the second-order dynamical equation of elastodynamics into an equivalent first-order system of coupled equations, so as to express the solution in the form of a Magnus expansion. With any spatial discretization, it entails computing the exponential of a matrix acting upon a vector. We employ an adaptive Krylov subspace approach to inexpensively and and accurately evaluate the action of the exponential matrix on a vector. In particular, we use an apriori error estimate to predict the optimal Kyrlov subspace size required for each time-step size. We show that the Magnus expansion truncated after its first term provides quadratic and superquadratic convergence in the time-step for nonlinear and linear elastodynamics, respectively. We demonstrate the accuracy and efficiency of the proposed method for one linear (linear cantilever beam) and three nonlinear (nonlinear cantilever beam, soft tissue elastomer, and hyperelastic rubber) benchmark systems. For a desired accuracy in energy, displacement, and velocity, our method allows for $10-100\times$ larger time-steps than conventional time-marching schemes such as Newmark-$\beta$ method. Computationally, it translates to a $\sim$$1000\times$ and $\sim$$10-100\times$ speed-up over conventional time-marching schemes for linear and nonlinear elastodynamics, respectively.