Equivariant Representation Learning via Class-Pose Decomposition

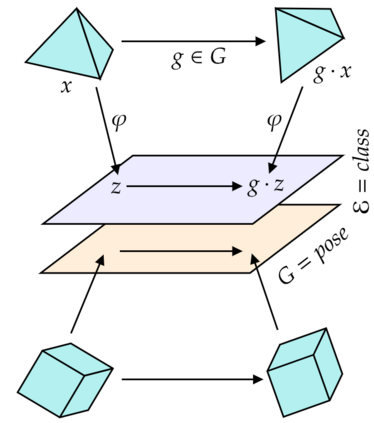
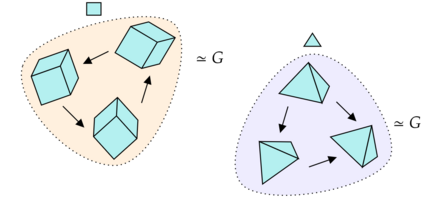
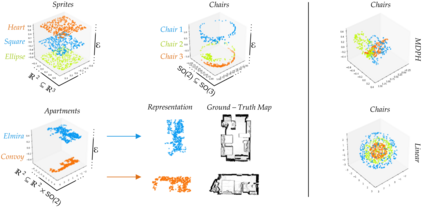
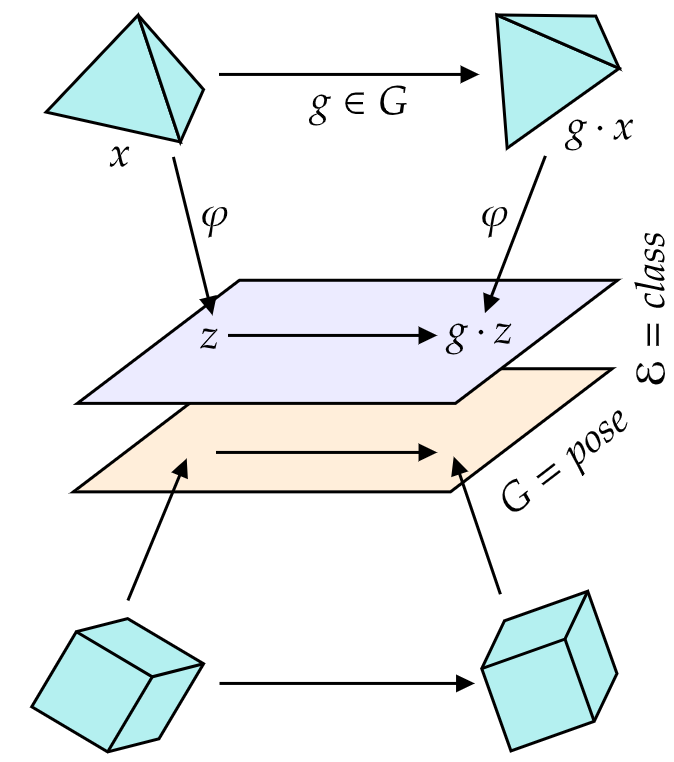
We introduce a general method for learning representations that are equivariant to symmetries of data. The central idea is to to decompose the latent space in an invariant factor and the symmetry group itself. The components semantically correspond to intrinsic data classes and poses respectively. The learner is self-supervised and infers these semantics based on relative symmetry information. The approach is motivated by theoretical results from group theory and guarantees representations that are lossless, interpretable and disentangled. We empirically investigate the approach via experiments involving datasets with a variety of symmetries. Results show that our representations capture the geometry of data and outperform other equivariant representation learning frameworks.