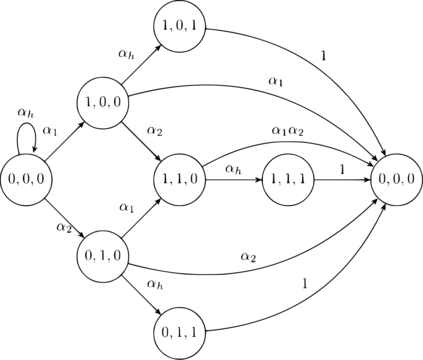
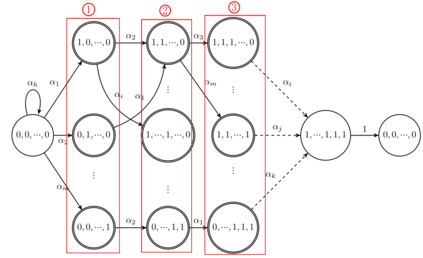
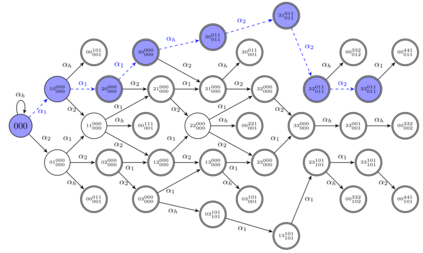
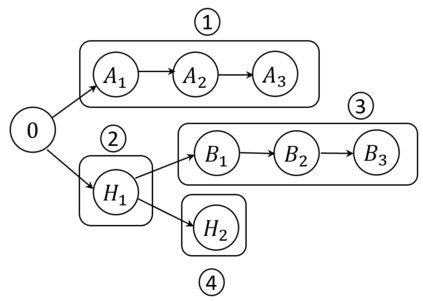
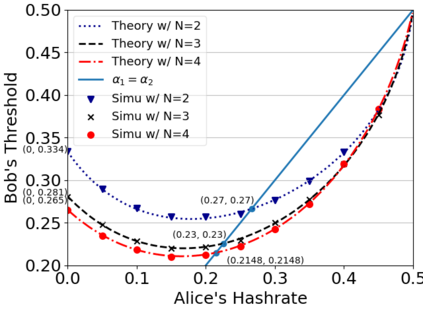
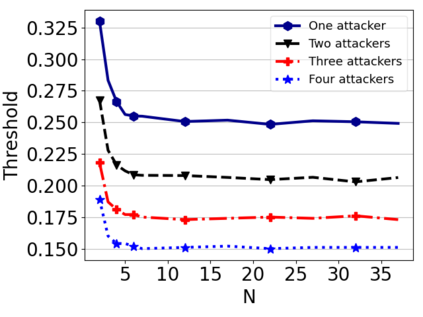
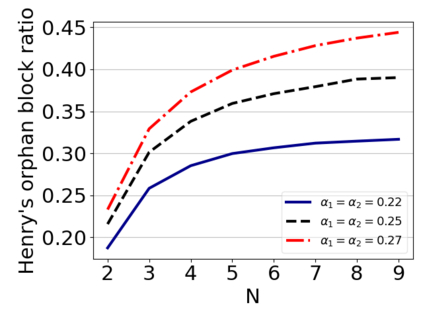
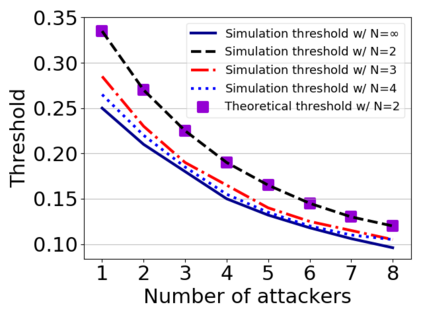
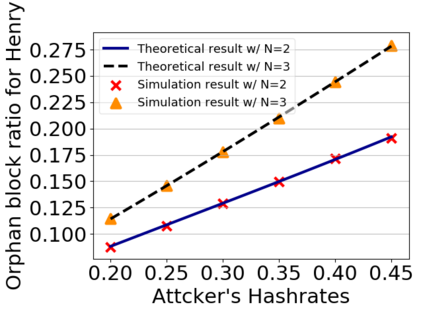
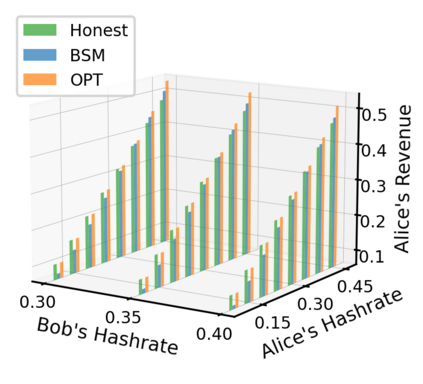
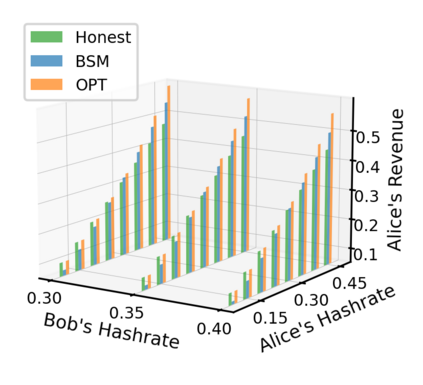
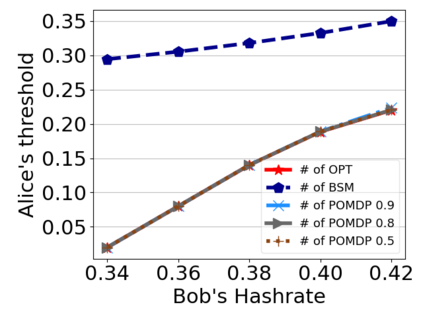
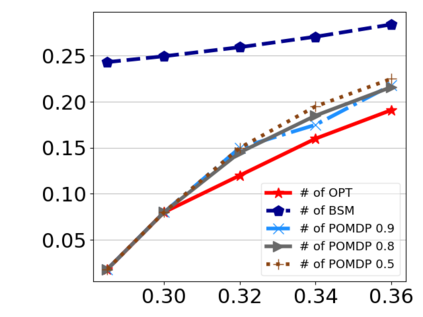
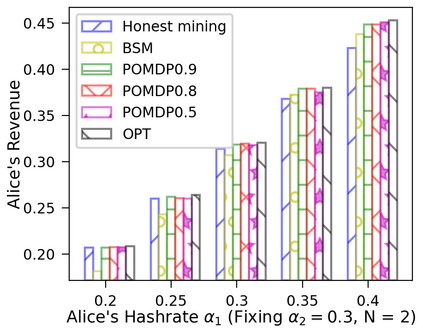
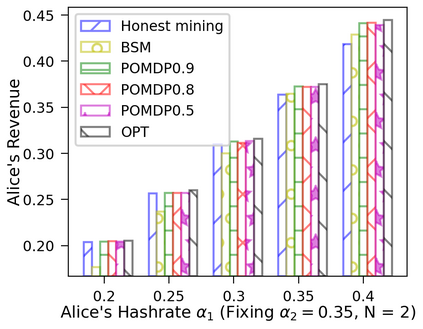
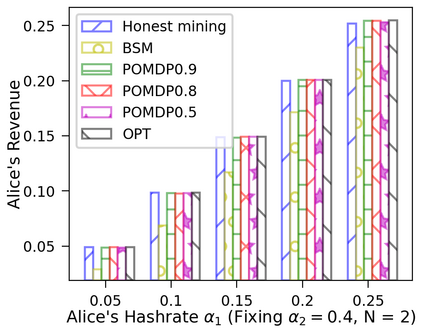
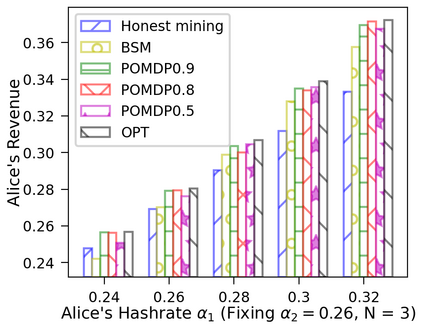
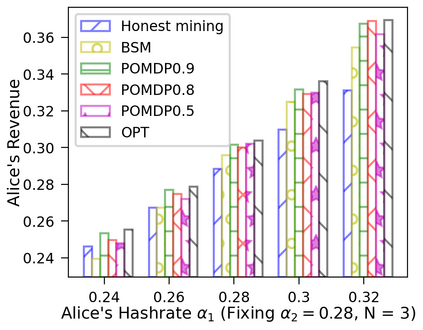
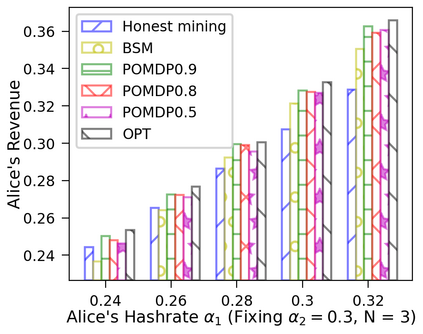
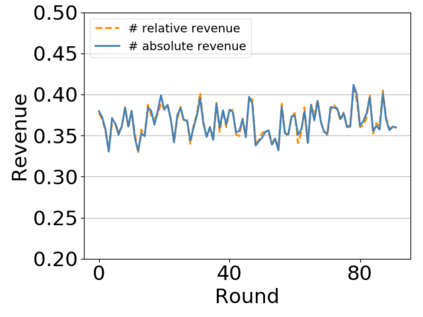
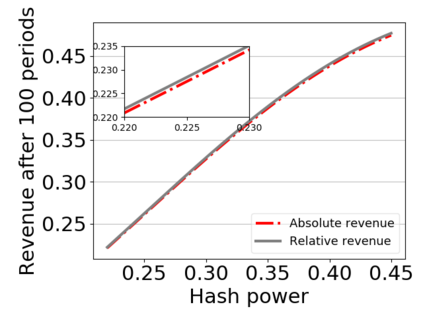
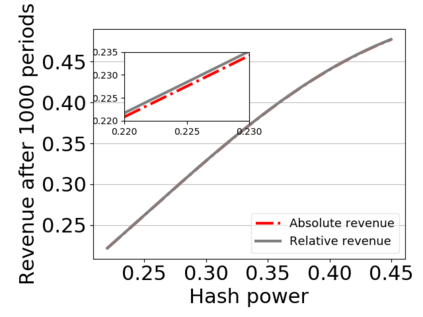
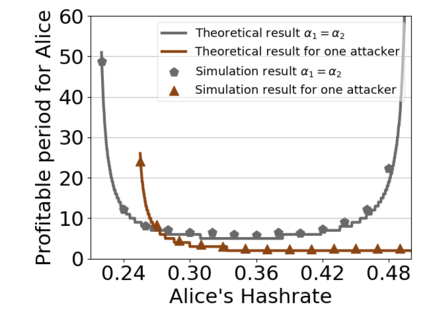
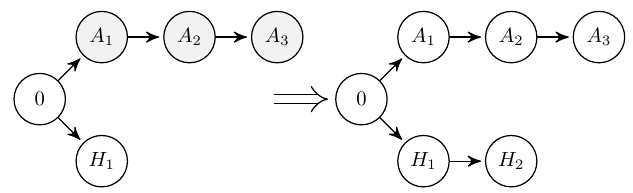
This paper studies a fundamental problem regarding the security of blockchain PoW consensus on how the existence of multiple misbehaving miners influences the profitability of selfish mining. Each selfish miner (or attacker interchangeably) maintains a private chain and makes it public opportunistically for acquiring more rewards incommensurate to his Hash power. We first establish a general Markov chain model to characterize the state transition of public and private chains for Basic Selfish Mining (BSM), and derive the stationary profitable threshold of Hash power in closed-form. It reduces from 25% for a single attacker to below 21.48% for two symmetric attackers theoretically, and further reduces to around 10% with eight symmetric attackers experimentally. We next explore the profitable threshold when one of the attackers performs strategic mining based on Partially Observable Markov Decision Process (POMDP) that only half of the attributes pertinent to a mining state are observable to him. An online algorithm is presented to compute the nearly optimal policy efficiently despite the large state space and high dimensional belief space. The strategic attacker mines selfishly and more agilely than BSM attacker when his Hash power is relatively high, and mines honestly otherwise, thus leading to a much lower profitable threshold. Last, we formulate a simple model of absolute mining revenue that yields an interesting observation: selfish mining is never profitable at the first difficulty adjustment period, but replying on the reimbursement of stationary selfish mining gains in the future periods. The delay till being profitable of an attacker increases with the decrease of his Hash power, making blockchain miners more cautious on performing selfish mining.
翻译:本文研究一个基本问题,即对于存在多种错误的矿工如何影响自私采矿利润的多重错误矿工的共识的安全问题。 每个自私的矿工(或攻击者可以互换)都维持一个私人链条,让公众有机会获得更多的奖赏,与哈什权力相配。我们首先建立一个通用的Markov链条模式,以描述基础自利采矿公司(BSM)公共和私人链条国家过渡的特点,并以封闭形式得出哈什电力固定的盈利门槛。它将一个单一攻击者的平均成本从25%降至21.48%以下,理论上说两个对称攻击者为21.48%以下,然后进一步降低到约10%左右的8个对称攻击者。我们接下来探索一个有利可图的门槛,当一名袭击者根据部分可观测的马尔科夫决定程序(POMDP)进行战略采矿时,只有与采矿国家有关的公私营和私人链条关系的一半属性是可见的。一个在线算法,尽管州际空间大,并且具有高度的信仰空间,但几乎是最佳的政策。战略攻击者对2个对2个对硫攻击者来说,其攻击者则更灵活、更精确地减少了10 %左右。 当我们开始对采矿进行绝对的观测时,一个真正的采矿税则开始一个更高的利润税期, 最终的利润期将比对采矿进行一个更高的利润期的利润期的利润期要开始一个更高的利润期的利润期。