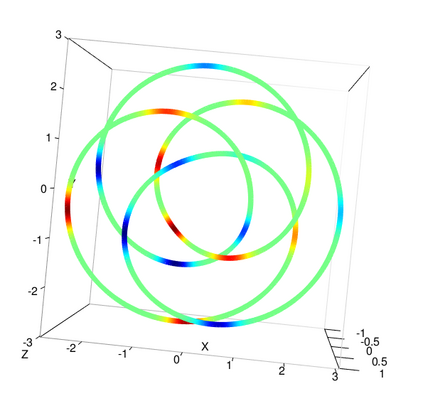
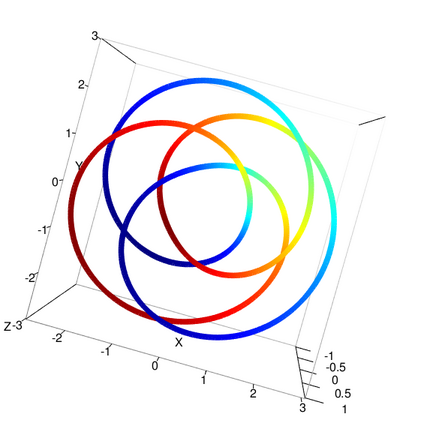
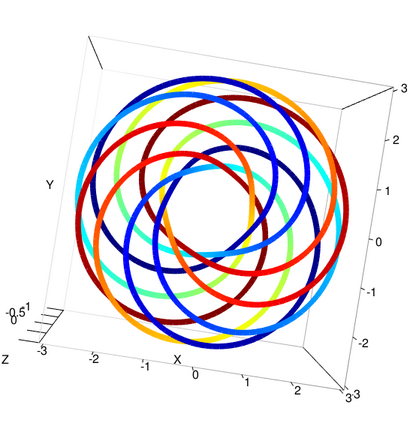
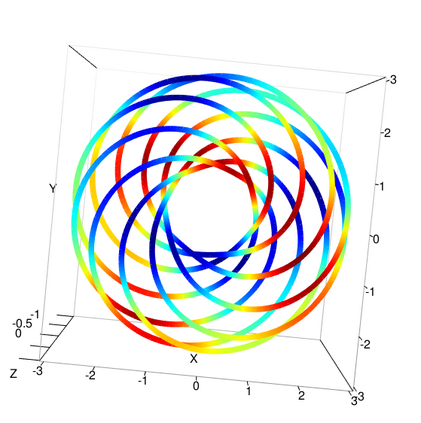
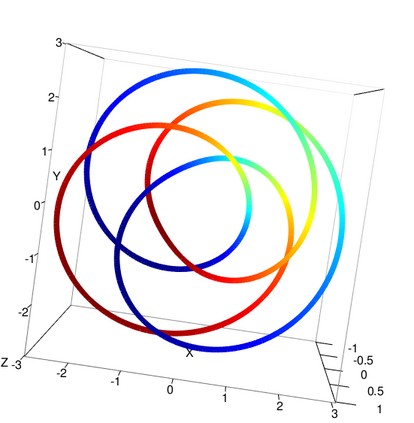
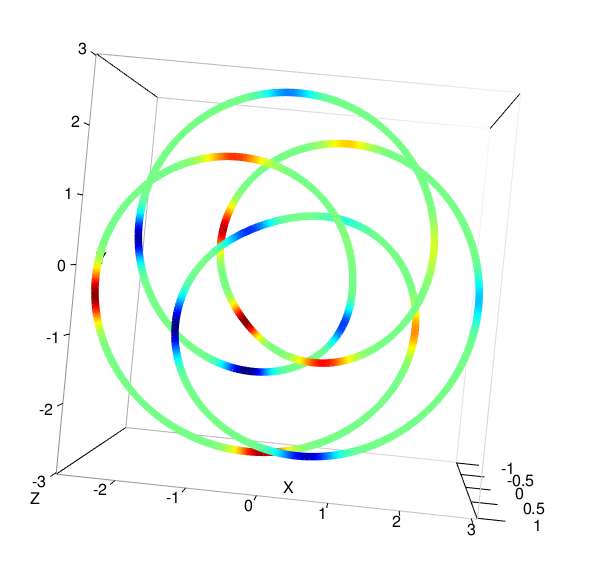
Amidst the growing interest in nonparametric regression, we address a significant challenge in Gaussian processes(GP) applied to manifold-based predictors. Existing methods primarily focus on low dimensional constrained domains for heat kernel estimation, limiting their effectiveness in higher-dimensional manifolds. Our research proposes an intrinsic approach for constructing GP on general manifolds such as orthogonal groups, unitary groups, Stiefel manifolds and Grassmannian manifolds. Our methodology estimates the heat kernel by simulating Brownian motion sample paths using the exponential map, ensuring independence from the manifold's embedding. The introduction of our strip algorithm, tailored for manifolds with extra symmetries, and the ball algorithm, designed for arbitrary manifolds, constitutes our significant contribution. Both algorithms are rigorously substantiated through theoretical proofs and numerical testing, with the strip algorithm showcasing remarkable efficiency gains over traditional methods. This intrinsic approach delivers several key advantages, including applicability to high dimensional manifolds, eliminating the requirement for global parametrization or embedding. We demonstrate its practicality through regression case studies (torus knots and eight dimensional projective spaces) and by developing binary classifiers for real world datasets (gorilla skulls planar images and diffusion tensor images). These classifiers outperform traditional methods, particularly in limited data scenarios.
翻译:暂无翻译