Memorization in Deep Neural Networks: Does the Loss Function matter?

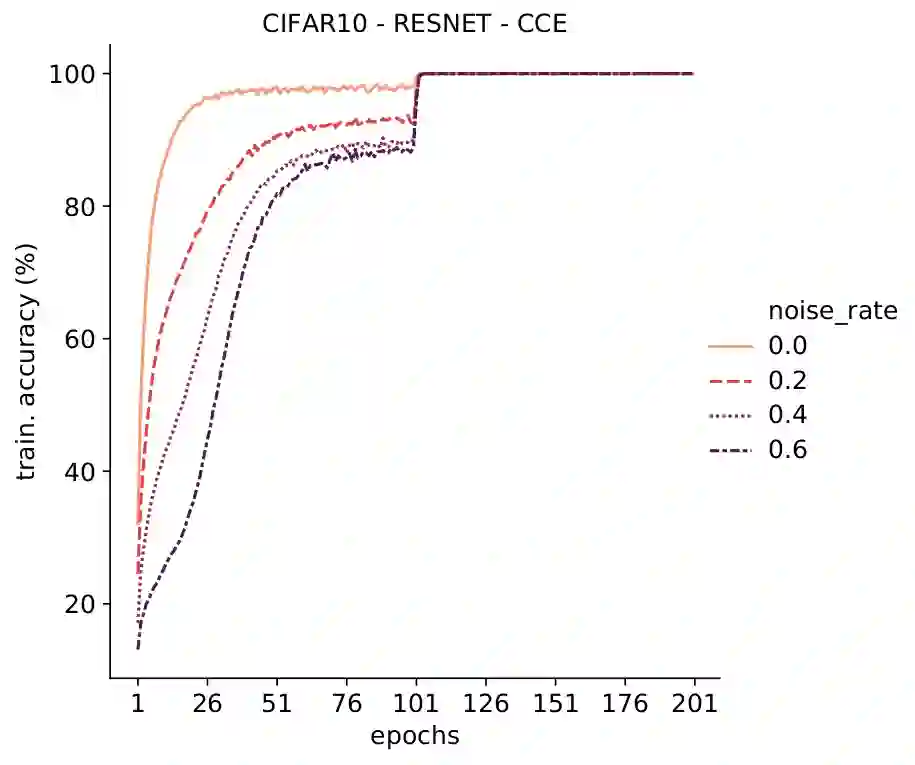
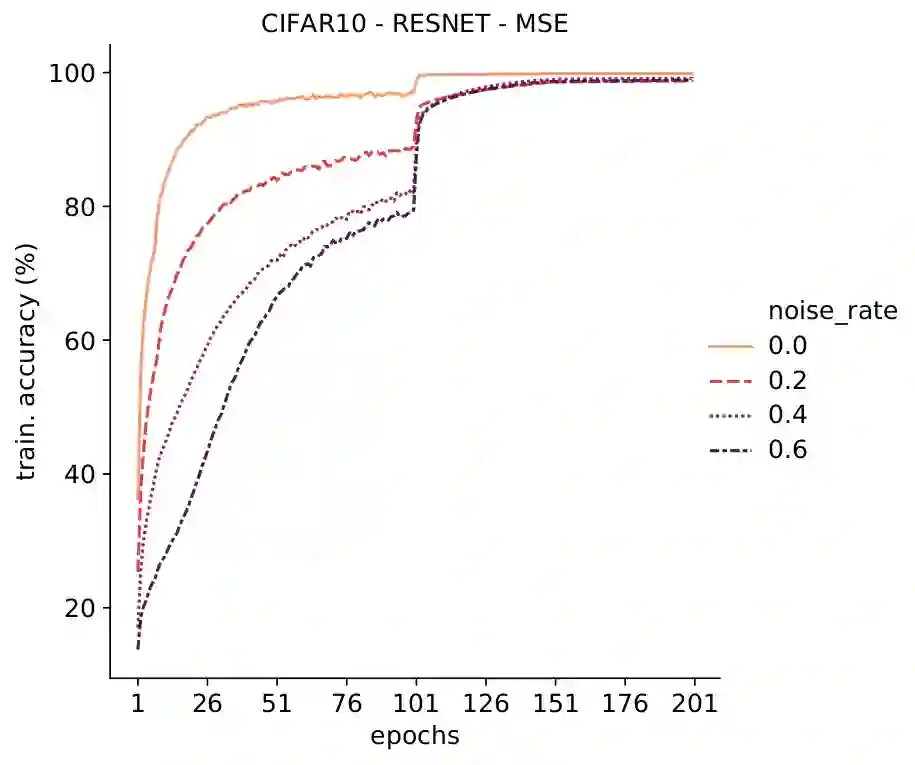
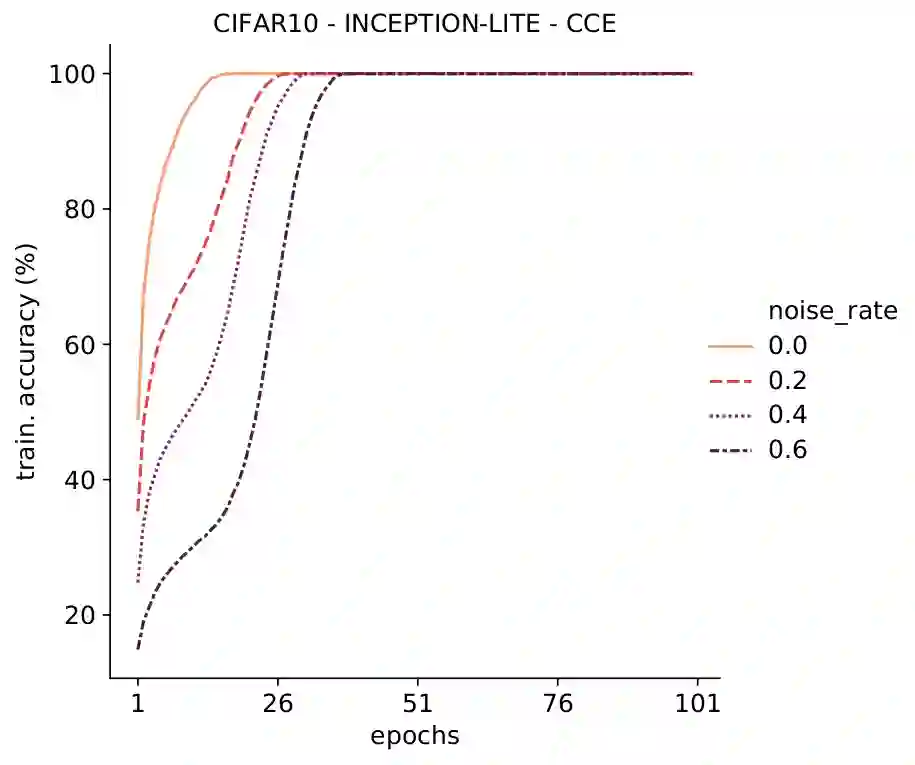
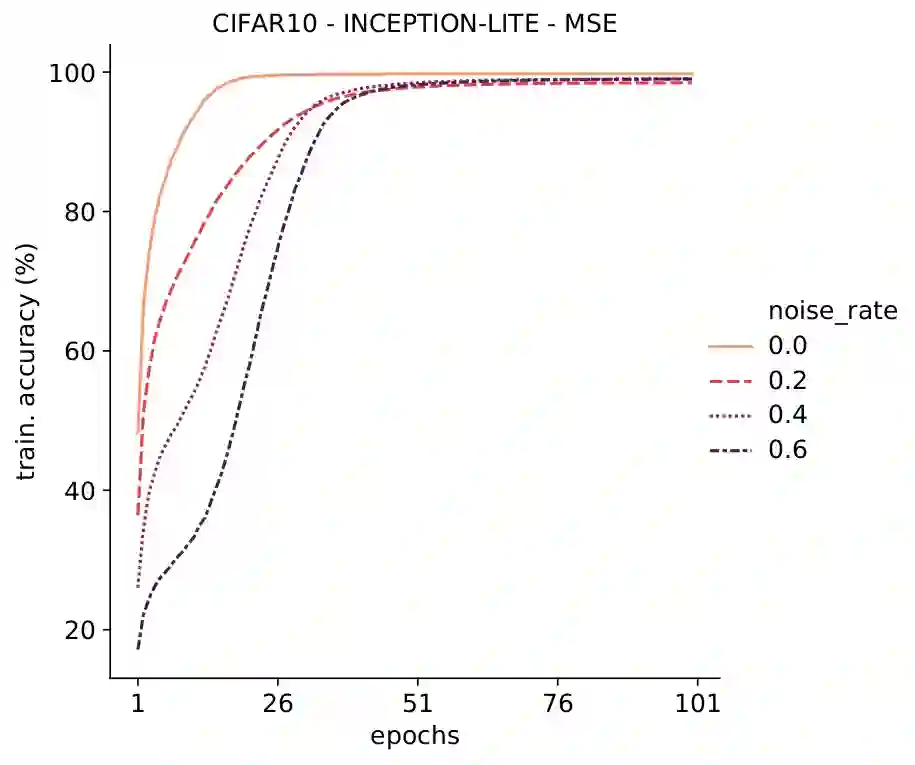
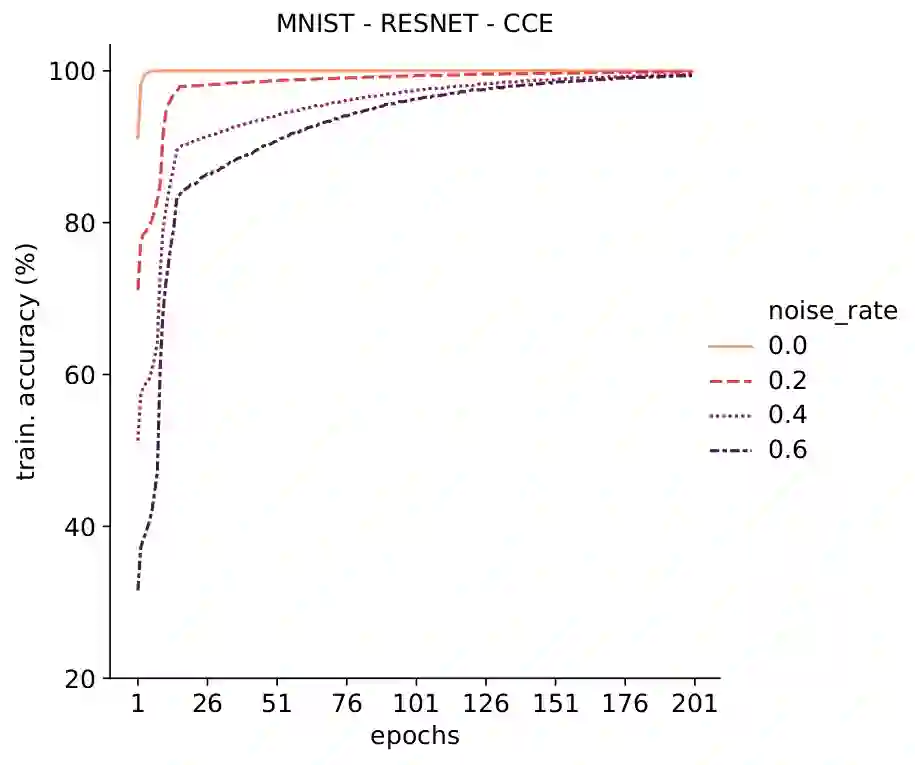
Deep Neural Networks, often owing to the overparameterization, are shown to be capable of exactly memorizing even randomly labelled data. Empirical studies have also shown that none of the standard regularization techniques mitigate such overfitting. We investigate whether the choice of the loss function can affect this memorization. We empirically show, with benchmark data sets MNIST and CIFAR-10, that a symmetric loss function, as opposed to either cross-entropy or squared error loss, results in significant improvement in the ability of the network to resist such overfitting. We then provide a formal definition for robustness to memorization and provide a theoretical explanation as to why the symmetric losses provide this robustness. Our results clearly bring out the role loss functions alone can play in this phenomenon of memorization.