A Fast Convergent Ordered-Subsets Algorithm with Subiteration-Dependent Preconditioners for PET Image Reconstruction

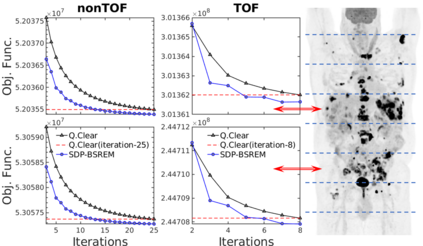
We investigated the imaging performance of a fast convergent ordered-subsets algorithm with subiteration-dependent preconditioners (SDPs) for positron emission tomography (PET) image reconstruction. In particular, we considered the use of SDP with the block sequential regularized expectation maximization (BSREM) approach with the relative difference prior (RDP) regularizer due to its prior clinical adaptation by vendors. Because the RDP regularization promotes smoothness in the reconstructed image, the directions of the gradients in smooth areas more accurately point toward the objective function's minimizer than those in variable areas. Motivated by this observation, two SDPs have been designed to increase iteration step-sizes in the smooth areas and reduce iteration step-sizes in the variable areas relative to a conventional expectation maximization preconditioner. The momentum technique used for convergence acceleration can be viewed as a special case of SDP. We have proved the global convergence of SDP-BSREM algorithms by assuming certain characteristics of the preconditioner. By means of numerical experiments using both simulated and clinical PET data, we have shown that our SDP-BSREM substantially improved the convergence rate, as compared to conventional BSREM and a vendor's implementation as Q.Clear. Specifically, in numerical experiments with a synthetic brain phantom, both proposed algorithms outperformed the conventional BSREM by a factor of two, while in experiments with clinical whole-body patient PET data (with and without time-of-flight information), the SDP-BSREM algorithm converged 35\%-50\% percent faster than the commercial Q.Clear algorithm.