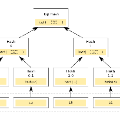
Commitment scheme is a central task in cryptography, where a party (typically called a prover) stores a piece of information (e.g., a bit string) with the promise of not changing it. This information can be accessed by another party (typically called the verifier), who can later learn the information and verify that it was not meddled with. Merkle tree is a well-known construction for doing so in a succinct manner, in which the verifier can learn any part of the information by receiving a short proof from the honest prover. Despite its significance in classical cryptography, there was no quantum analog of the Merkle tree. A direct generalization using the Quantum Random Oracle Model (QROM) does not seem to be secure. In this work, we propose the quantum Merkle tree. It is based on what we call the Quantum Haar Random Oracle Model (QHROM). In QHROM, both the prover and the verifier have access to a Haar random quantum oracle G and its inverse. Using the quantum Merkle tree, we propose a succinct quantum argument for the Gap-k-Local-Hamiltonian problem. We prove it is secure against semi-honest provers in QHROM and conjecture its general security. Assuming the Quantum PCP conjecture is true, this succinct argument extends to all of QMA. This work raises a number of interesting open research problems.
翻译:在加密中,承诺方案是一项核心任务,即一方(通常称为证明人)储存了一块信息(例如,一小块字符串),并承诺不更改这些信息。另一个当事方(通常称为核查人)可以获取这些信息,后者后来可以学习这些信息,并核实这些信息没有被调用过。Merkle树是以简洁的方式这样做的著名建筑,核查人可以通过从诚实证明人那里获得一个简短的证据来了解信息的任何部分。尽管它在古典加密中具有意义,但Merkle树没有量的类比。使用Qalkle随机甲骨模型(QROM)的直接概括化似乎并不安全。在这项工作中,我们建议使用量子Merkle树,以我们称之为Qantum Haar 随机Oracle模型(QHROM)的精确结构。在Qrkle Kroup-Cal-Cal-Conalum Grouproup Group 上,我们提出一个简明的硬度的硬度的硬度标度论证。</s>