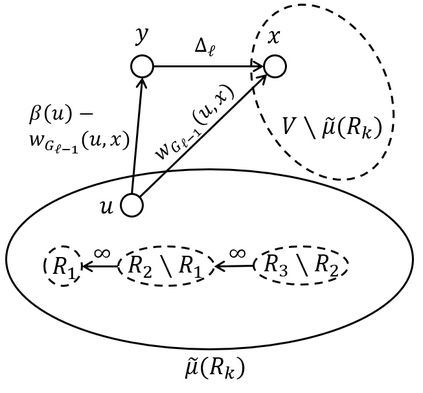
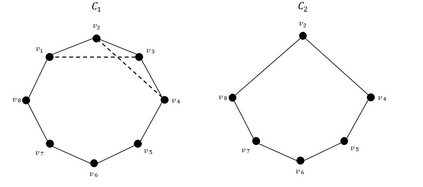
We give an almost-linear time algorithm for the Steiner connectivity augmentation problem: given an undirected graph, find a smallest (or minimum weight) set of edges whose addition makes a given set of terminals $\tau$-connected (for any given $\tau > 0$). The running time of our algorithm is dominated by polylogarithmic calls to any maximum flow subroutine; using the recent almost-linear time maximum flow algorithm (Chen et al., FOCS 2022), we get an almost-linear running time for our algorithm as well. This is tight up to the polylogarithmic factor even for just two terminals. Prior to our work, an almost-linear (in fact, near-linear) running time was known only for the special case of global connectivity augmentation, i.e., when all vertices are terminals (Cen et al., STOC 2022). We also extend our algorithm to the closely related Steiner splitting-off problem, where the edges incident on a vertex have to be {\em split-off} while maintaining the (Steiner) connectivity of a given set of terminals. Prior to our work, a nearly-linear time algorithm was known only for the special case of global connectivity (Cen et al., STOC 2022). The only known generalization beyond global connectivity was to preserve all pairwise connectivities using a much slower algorithm that makes $n$ calls to an all-pairs maximum flow (or Gomory-Hu tree) subroutine (Lau and Yung, SICOMP 2013), as against polylog(n) calls to a (single-pair) maximum flow subroutine in this work.
翻译:我们给施泰纳连通性增强问题提供了几乎线性时间算法:鉴于一个没有方向的图表,我们找到一组最小(或最小重量)的边缘,这些边缘的添加使得一组特定的终端 $\ tau$-连通(对于任何给定的$tau > 0美元)。我们算法的运行时间主要取决于任何最大流流次路径的多线性呼唤;使用最近几乎线性时间最大流算法(Chen等人,FOCS 2022),我们得到一个几乎线性运行的时间,我们的算法也几乎线性运行时间。这甚至接近于两个端点的多线性因素。在我们工作之前,一个几乎线性(事实上,近线性)运行时间只为全球连通性增强的特例,即当所有脊椎都是终点时(Cen等人,STOC 2022)。我们还将我们的Stalogyal 算法只延伸到密切关联的 Steiner-blick-dal-ality问题(Sildality, iver iot river rient river river river river) 不得不一个离离子事件不得不-al-al-al-al-al-revental-rations) 几乎一个小的离不开一个小路流,近C-ral-ral-ral-ral-lent-ral-ral-ral-ral-lent-ral-ral-ral-ral-ral-tal-tal-tal-tal-lation-tal-tal-tal-lick-lick-lick-t-t-t-t-s-s-s-s-s-s-s-s-s-s-s-n-n-n-n-n-s-n-n-n-n-n-s-n-n-n-n-s-s-n-n-n-n-n-s-s-n-n-n-n-n-n-s-s-s-s-s-s-n-s-l-l-l-l-l-l-l-l-l-l-l-l-l-l-