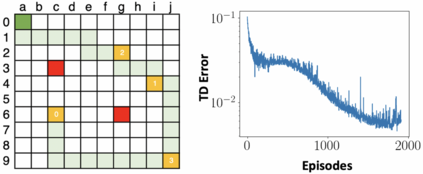
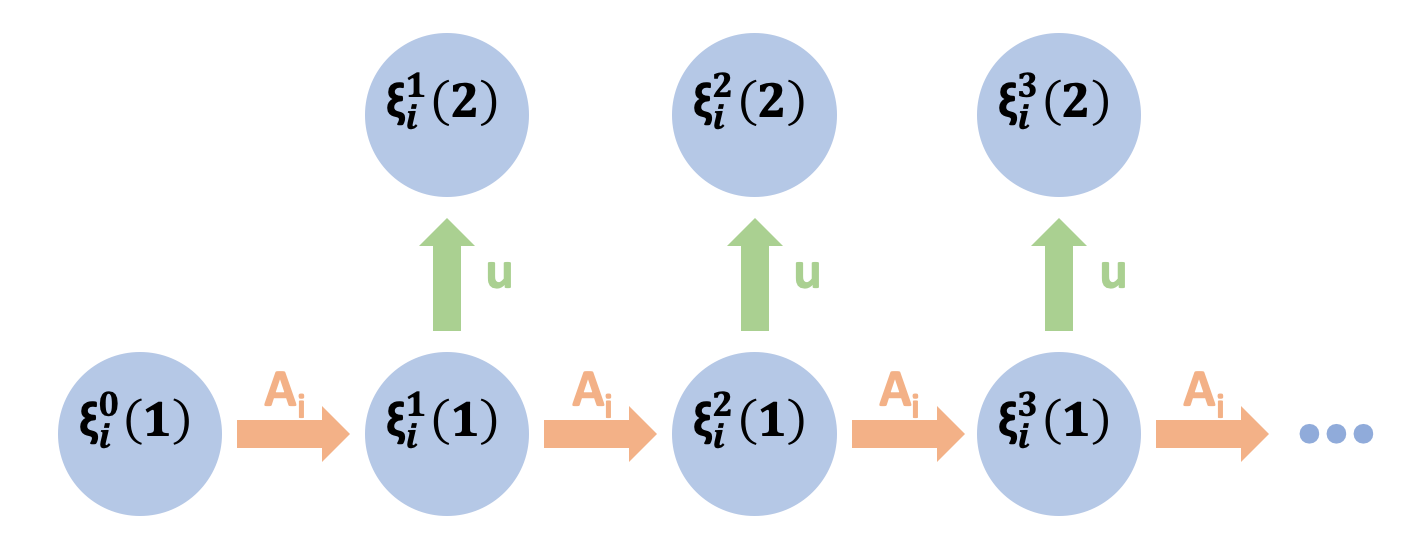
We study a decentralized variant of stochastic approximation, a data-driven approach for finding the root of an operator under noisy measurements. A network of agents, each with its own operator and data observations, cooperatively find the fixed point of the aggregate operator over a decentralized communication graph. Our main contribution is to provide a finite-time analysis of this decentralized stochastic approximation method when the data observed at each agent are sampled from a Markov process; this lack of independence makes the iterates biased and (potentially) unbounded. Under fairly standard assumptions, we show that the convergence rate of the proposed method is essentially the same as if the samples were independent, differing only by a log factor that accounts for the mixing time of the Markov processes. The key idea in our analysis is to introduce a novel Razumikhin-Lyapunov function, motivated by the one used in analyzing the stability of delayed ordinary differential equations. We also discuss applications of the proposed method on a number of interesting learning problems in multi-agent systems.
翻译:我们研究的是一种分散式的随机近似法,这是一种数据驱动法,用于寻找在噪音测量下操作者的根源。一个由各种物剂组成的网络,每个物剂都有自己的操作者和数据观测,在分散式通信图中合作找到总操作者的固定点。我们的主要贡献是,当每个物剂所观察到的数据从Markov过程取样时,对这种分散式的随机近似法进行有一定的时间分析;这种缺乏独立性使迭代产生偏向,(可能)不受约束。根据相当标准的假设,我们表明,拟议方法的趋同率基本上与样本是独立的一样,只有计算Markov过程混合时间的日志因素才有所不同。我们分析中的关键思想是引入一个新颖的Razumikhin-Lyapunov功能,其动机是用来分析延迟的普通差异方程式的稳定性。我们还讨论了在多试剂系统中对一些有趣的学习问题采用拟议方法的情况。