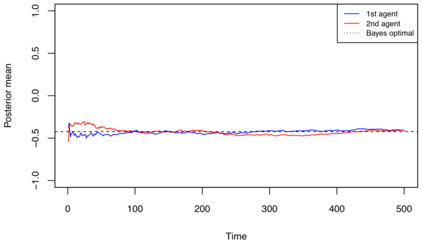
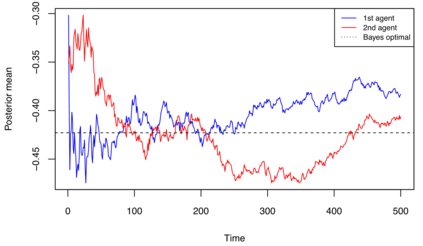
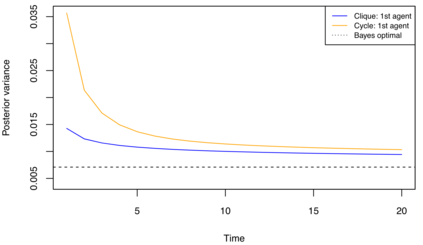
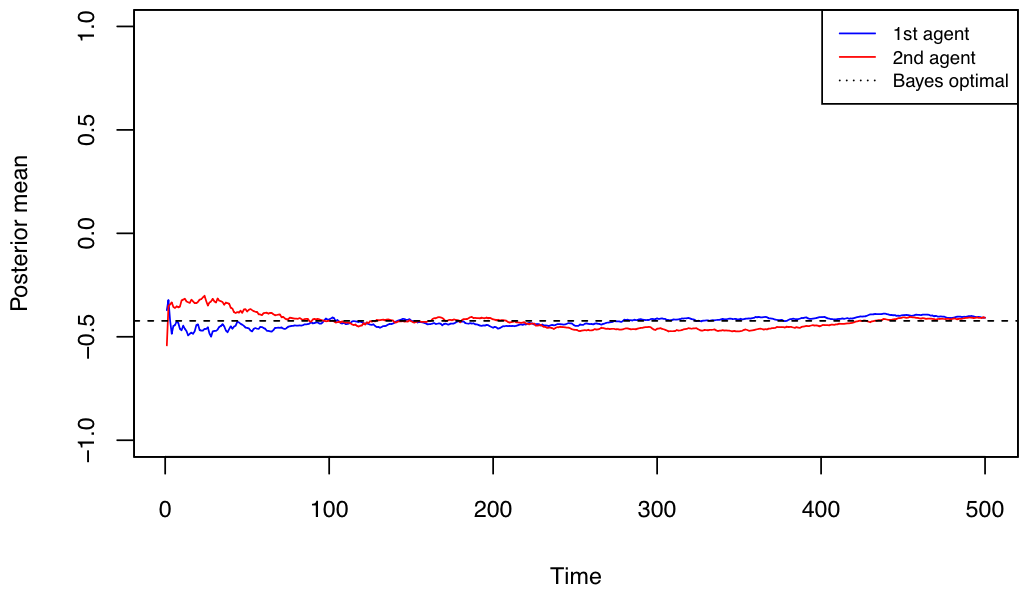
Bayesian models of group learning are studied in Economics since the 1970s. and more recently in computational linguistics. The models from Economics postulate that agents maximize utility in their communication and actions. The Economics models do not explain the ``probability matching" phenomena that are observed in many experimental studies. To address these observations, Bayesian models that do not formally fit into the economic utility maximization framework were introduced. In these models individuals sample from their posteriors in communication. In this work we study the asymptotic behavior of such models on connected networks with repeated communication. Perhaps surprisingly, despite the fact that individual agents are not utility maximizers in the classical sense, we establish that the individuals ultimately agree and furthermore show that the limiting posterior is Bayes optimal. We explore the interpretation of our results in terms of Large Language Models (LLMs). In the positive direction our results can be interpreted as stating that interaction between different LLMs can lead to optimal learning. However, we provide an example showing how misspecification may lead LLM agents to be overconfident in their estimates.
翻译:暂无翻译