Feasible Adjustments of Statistical Inference in High-Dimensional Generalized Linear Models

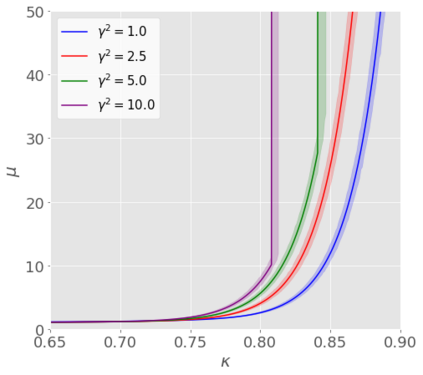
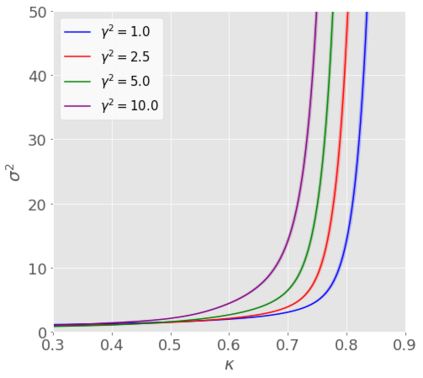
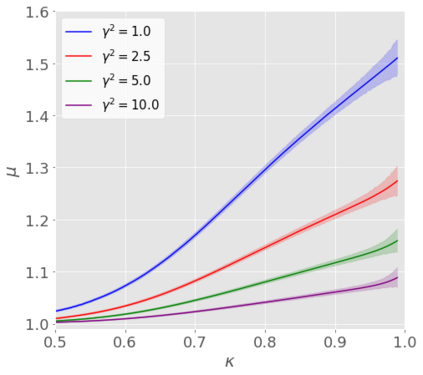
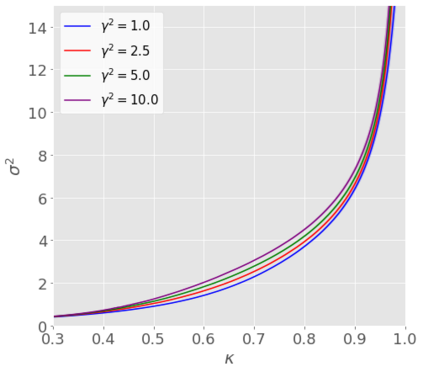
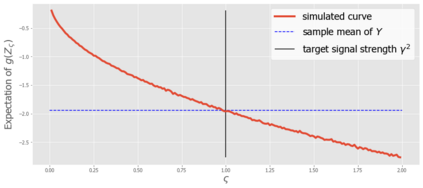
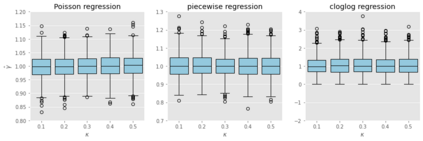
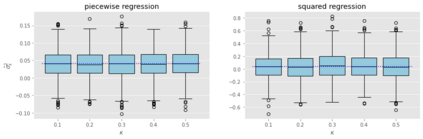
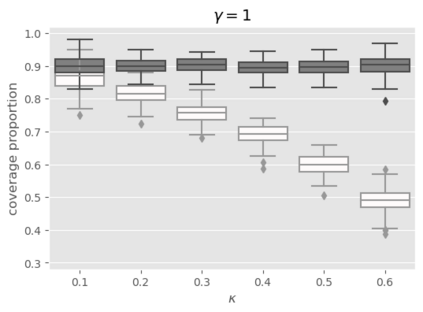
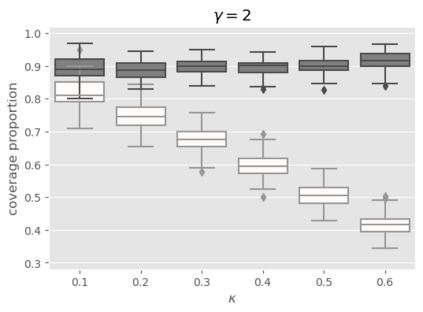
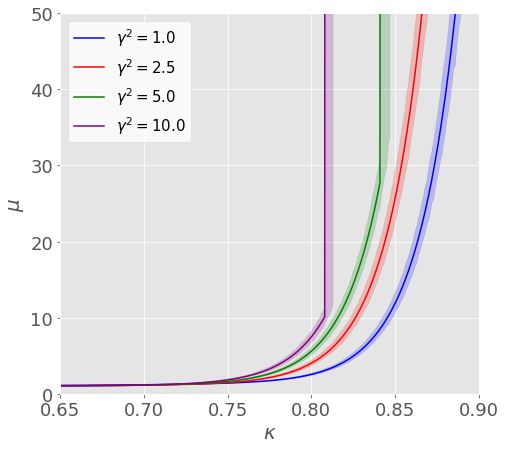
We developed a statistical inference method applicable to a broad range of generalized linear models (GLMs) in high-dimensional settings, where the number of unknown coefficients scales proportionally with the sample size. Although a pioneering inference method has been developed for logistic regression, which is a specific instance of GLMs, it is not feasible to apply this method directly to other GLMs because of unknown hyper-parameters. In this study, we addressed this limitation by developing a new inference method designed for a certain class of GLMs. Our method is based on the adjustment of asymptotic normality in high dimensions and is feasible in the sense that it is possible even with unknown hyper-parameters. Specifically, we introduce a novel convex loss-based estimator and its associated system, which are essential components of inference. Next, we devise a methodology for identifying the system parameters required by the method. Consequently, we construct confidence intervals for GLMs in a high-dimensional regime. We prove that our proposed method has desirable theoretical properties, such as strong consistency and exact coverage probability. Finally, we experimentally confirmed its validity.