Well balanced finite volume schemes for shallow water equations on manifolds

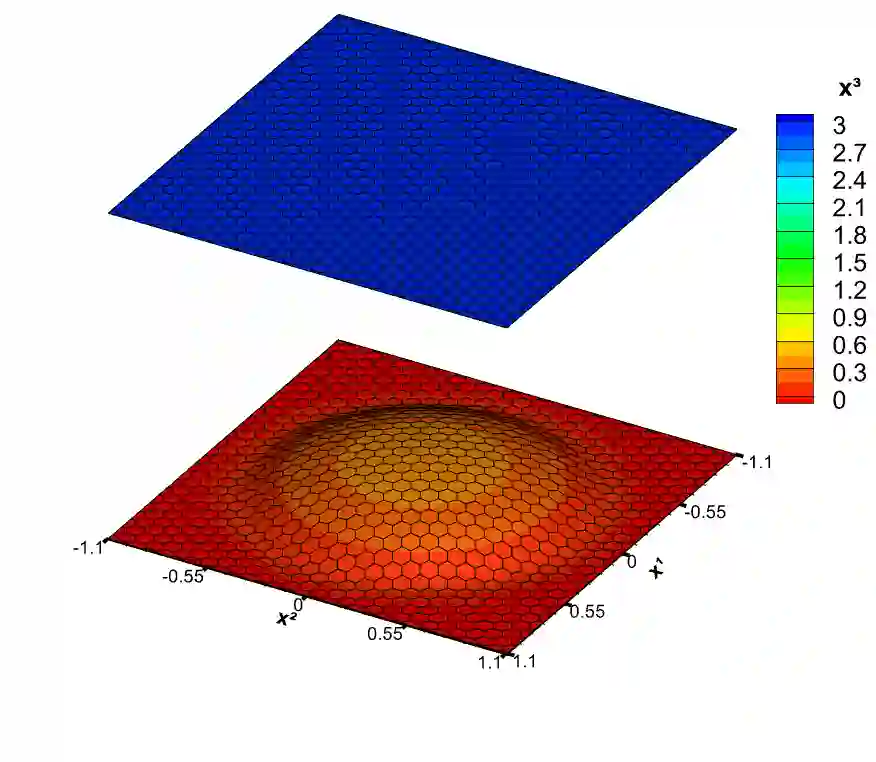
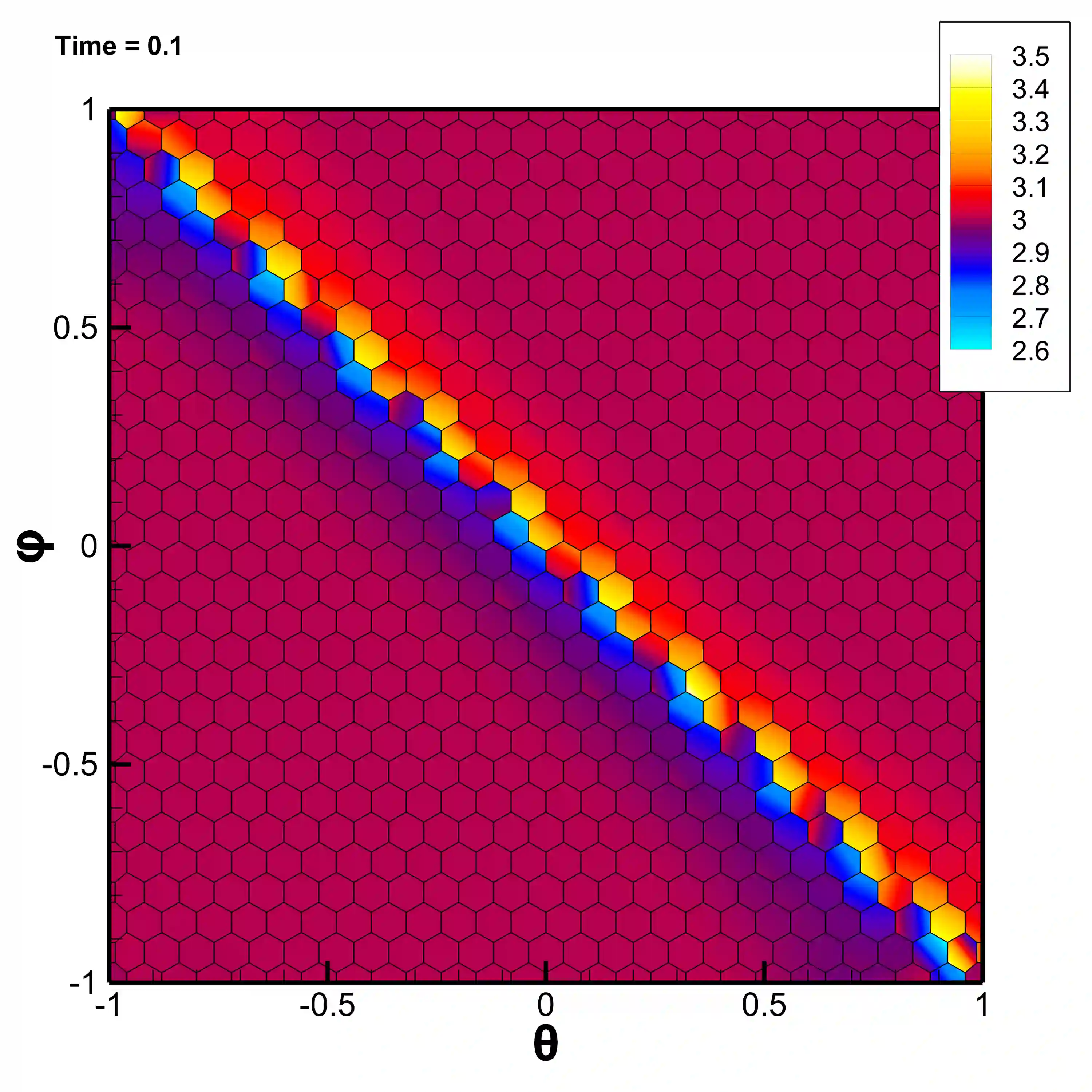
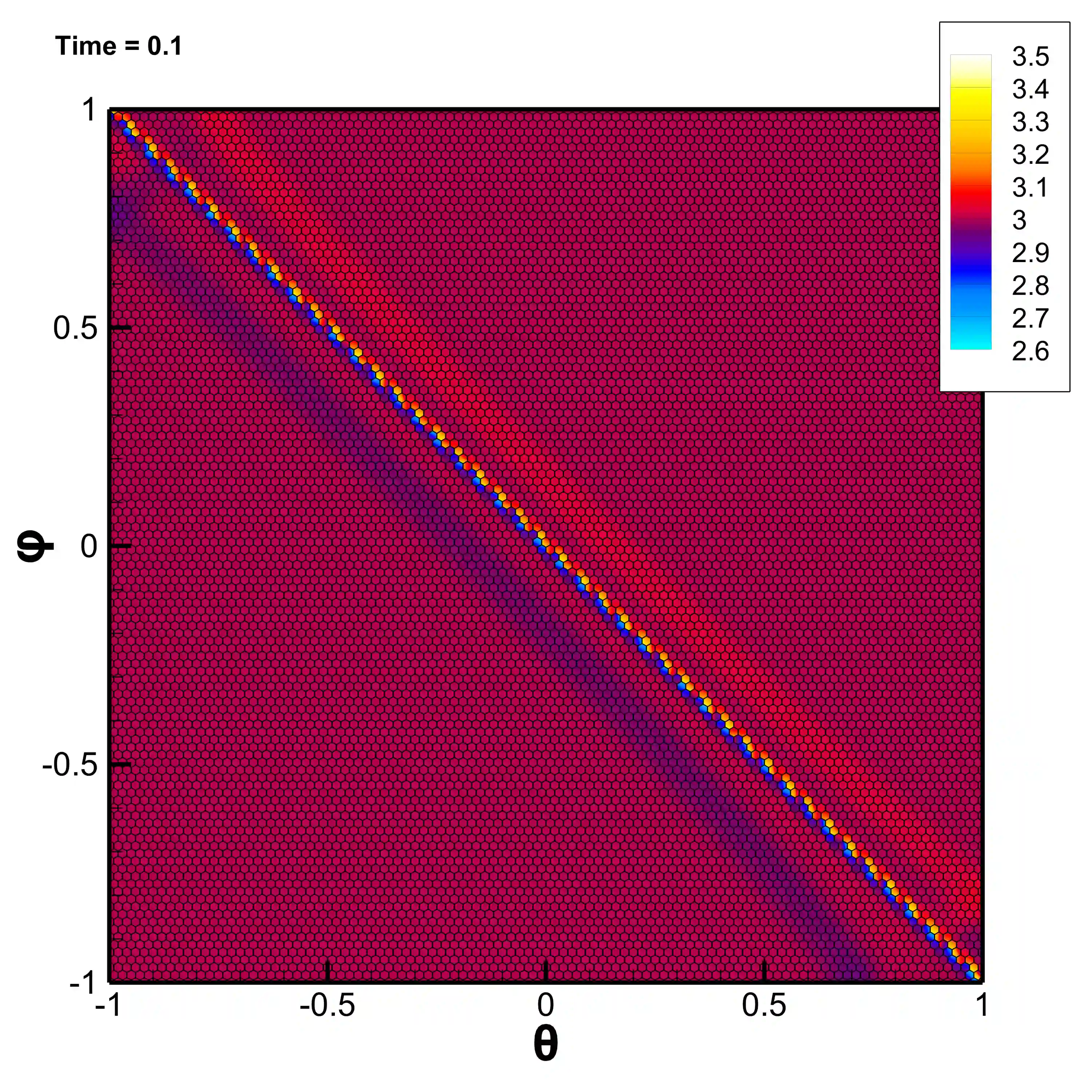
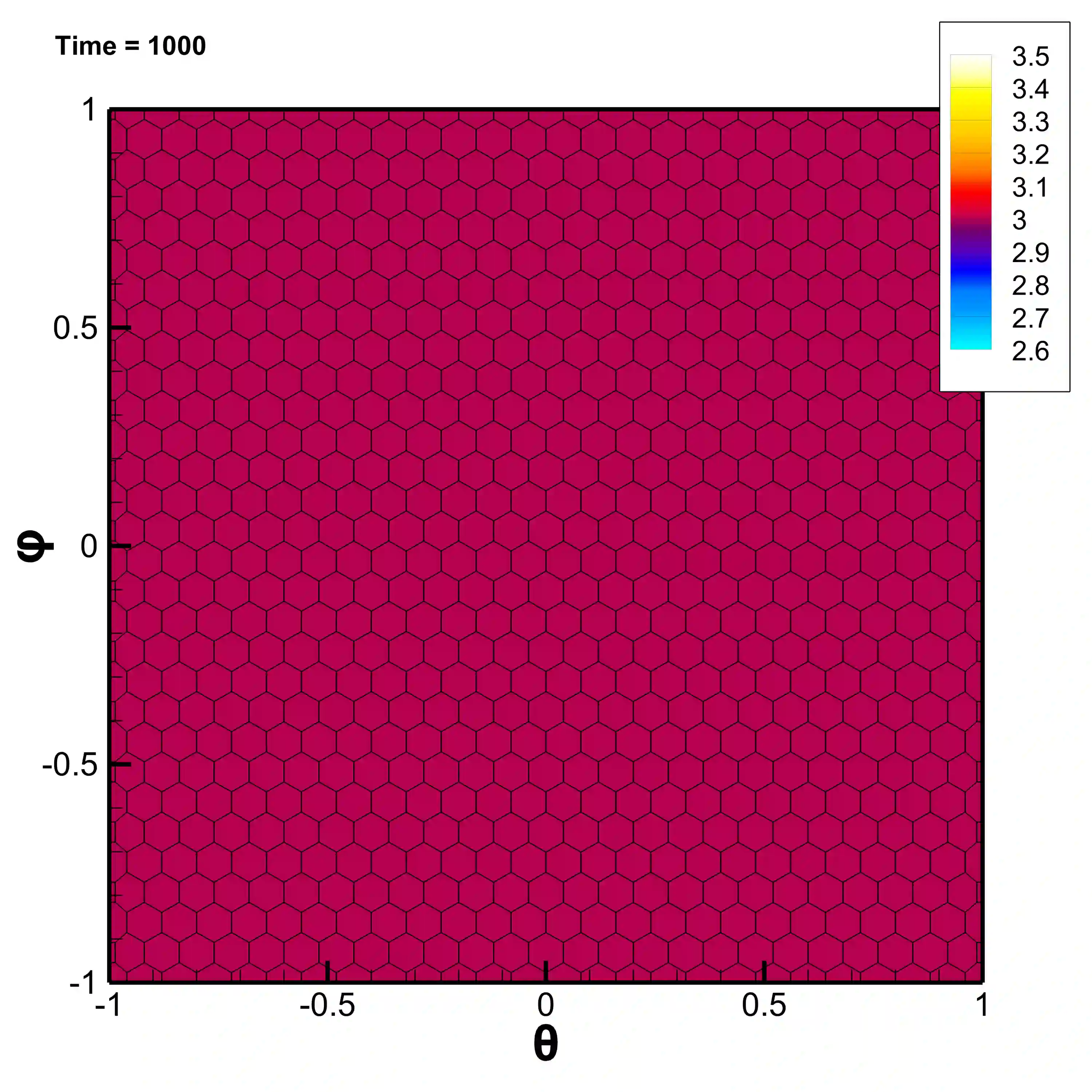
In this paper we propose a novel second-order accurate well balanced scheme for shallow water equations in general covariant coordinates over manifolds. In our approach, once the gravitational field is defined for the specific case, one equipotential surface is detected and parametrized by a frame of general covariant coordinates. This surface is the manifold whose covariant parametrization induces a metric tensor. The model is then re-written in a hyperbolic form with a tuple of conserved variables composed both of the evolving physical quantities and the metric coefficients. This formulation allows the numerical scheme to automatically compute the curvature of the manifold as long as the physical variables are evolved.