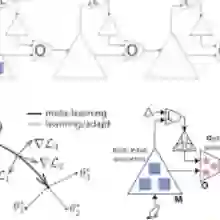
Meta-learning owns unique effectiveness and swiftness in tackling emerging tasks with limited data. Its broad applicability is revealed by viewing it as a bi-level optimization problem. The resultant algorithmic viewpoint however, faces scalability issues when the inner-level optimization relies on gradient-based iterations. Implicit differentiation has been considered to alleviate this challenge, but it is restricted to an isotropic Gaussian prior, and only favors deterministic meta-learning approaches. This work markedly mitigates the scalability bottleneck by cross-fertilizing the benefits of implicit differentiation to probabilistic Bayesian meta-learning. The novel implicit Bayesian meta-learning (iBaML) method not only broadens the scope of learnable priors, but also quantifies the associated uncertainty. Furthermore, the ultimate complexity is well controlled regardless of the inner-level optimization trajectory. Analytical error bounds are established to demonstrate the precision and efficiency of the generalized implicit gradient over the explicit one. Extensive numerical tests are also carried out to empirically validate the performance of the proposed method.
翻译:元学习在处理具有受限数据的新兴任务时具有高效性和迅捷性。尽管将其视为二级优化问题使算法视角更加鲜明,但当内层优化依赖于基于梯度的迭代时,仍面临着可扩展性问题。隐式求导被认为可以缓解这一挑战,但它仅限于各向同性高斯先验,并且只有确定性元学习方法受益。本文通过跨界发掘隐式求导的优势,显著缓解了可扩展性瓶颈,将其应用于概率贝叶斯元学习。新颖的隐式贝叶斯元学习(iBaML)方法不仅扩展了可学习先验的范围,而且还量化了相关不确定性。此外,无论内层优化轨迹如何,最终复杂性都得到很好的控制。分析误差界定已经预示了广义隐式梯度对比显式梯度的精确性和效率。此外,还进行了大量的数字测试,以验证所提出方法的性能。