Codes for Preventing Zeros at Partially Defect Memory Positions

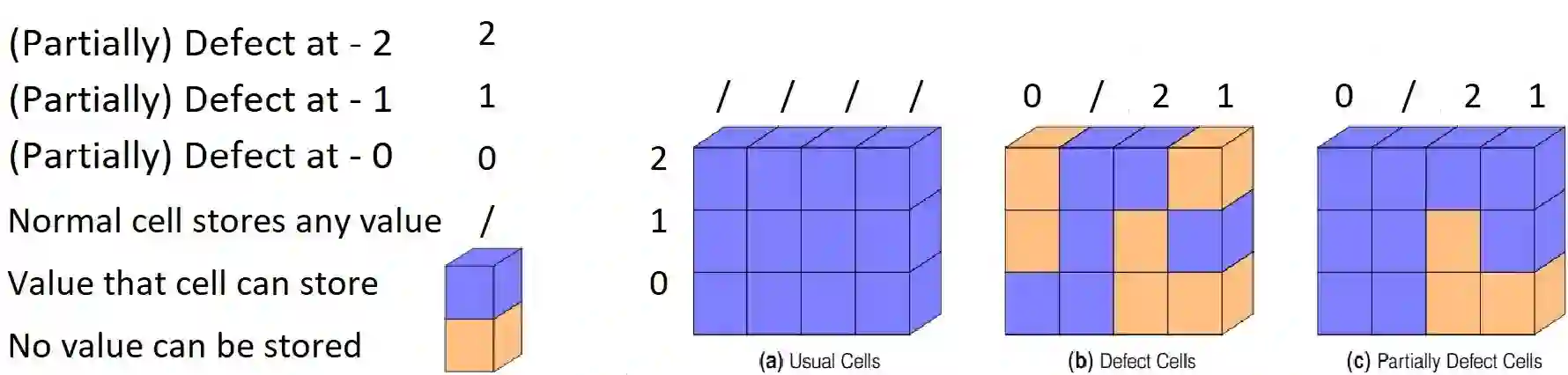
This work deals with error correction for non-volatile memories that are partially defect-at some levels. Such memory cells can only store incomplete information since some of their levels cannot be utilized entirely due to, e.g. wearout. On top of that, this paper corrects random errors $t\geq 1$ that could happen among $u$ partially defective cells while preserving their constraints. First, we show that the probability of violating the partially defective cells' restriction due to random errors is not trivial. Next, we update the models in [1] such that the coefficients of the output encoded vector plus the error vector at the partially defect positions are nonzero. Lastly, we state a simple theorem for masking the partial defects using a code with a minimum distance $d$ such that $d\geq (u+t)+1$. "Masking" means selecting a word whose entries correspond to writable levels in the (partially) defect positions. A comparison shows that, for a certain BCH code, masking $u$ cells by this theorem is as good as using the complicated coding scheme proven in [1, Theorem 1].