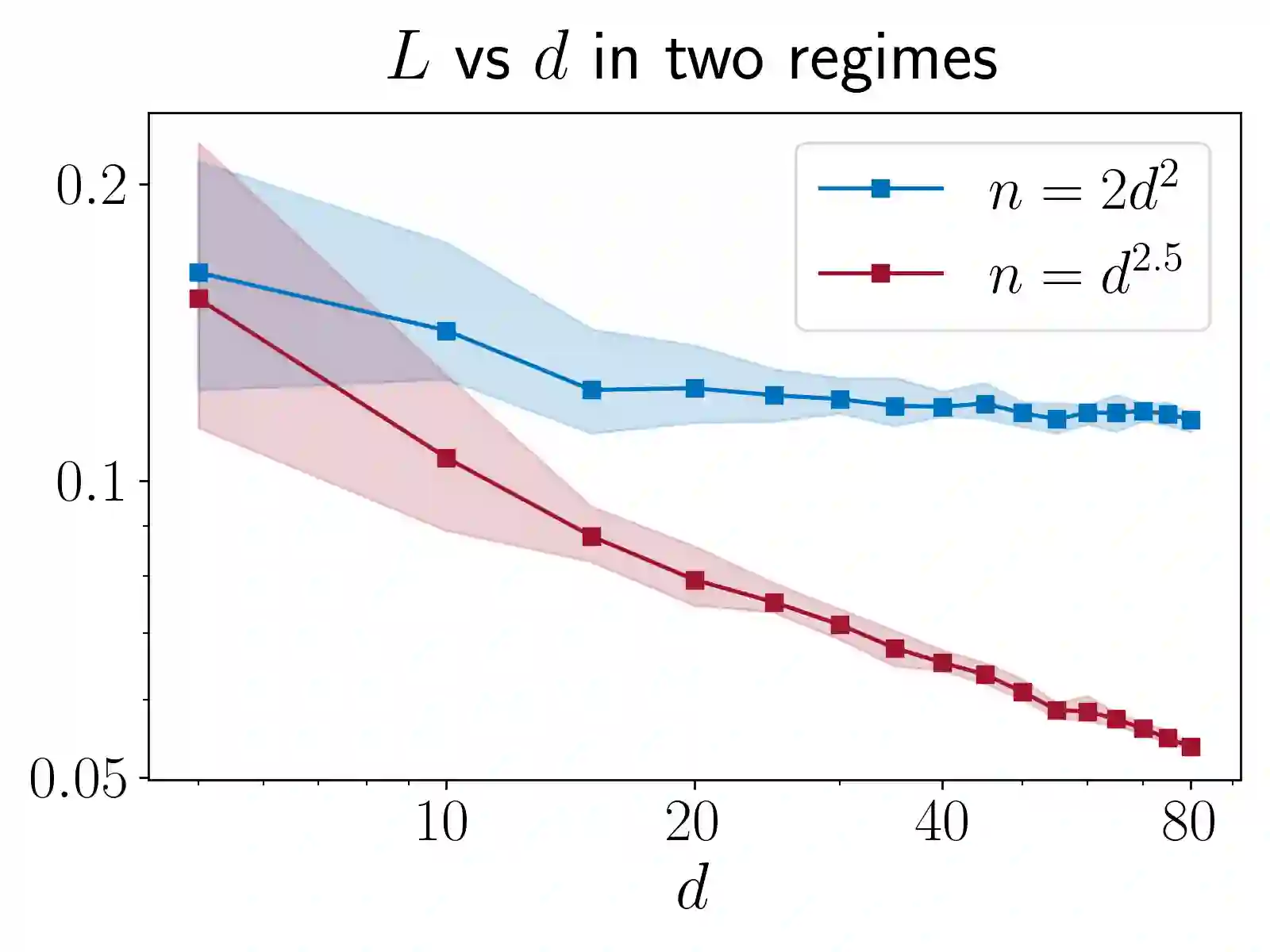
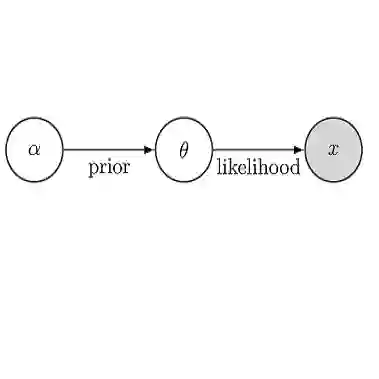
In Bayesian inference, a widespread technique to compute integrals against a high-dimensional posterior is to use a Gaussian proxy to the posterior known as the Laplace approximation. We address the question of accuracy of the approximation in terms of TV distance, in the regime in which dimension $d$ grows with sample size $n$. Multiple prior works have shown the requirement $d^3\ll n$ is sufficient for accuracy of the approximation. But in a recent breakthrough, Kasprzak et al, 2022 derived an upper bound scaling as $d/\sqrt n$. In this work, we further refine our understanding of the Laplace approximation error by decomposing the TV error into an $O(d/\sqrt n)$ leading order term, and an $O(d^2/n)$ remainder. This decomposition has far reaching implications: first, we use it to prove that the requirement $d^2\ll n$ cannot in general be improved by showing TV$\gtrsim d/\sqrt n$ for a posterior stemming from logistic regression with Gaussian design. Second, the decomposition provides tighter and more easily computable upper bounds on the TV error. Our result also opens the door to proving the BvM in the $d^2\ll n$ regime, and correcting the Laplace approximation to account for skew; this is pursued in two follow-up works.
翻译:暂无翻译