An integer programming approach for solving a generalized version of the Grundy domination number

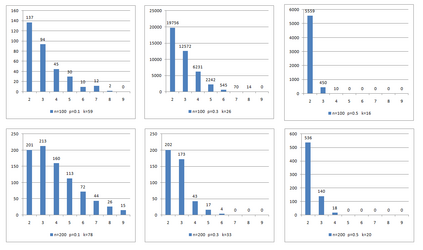
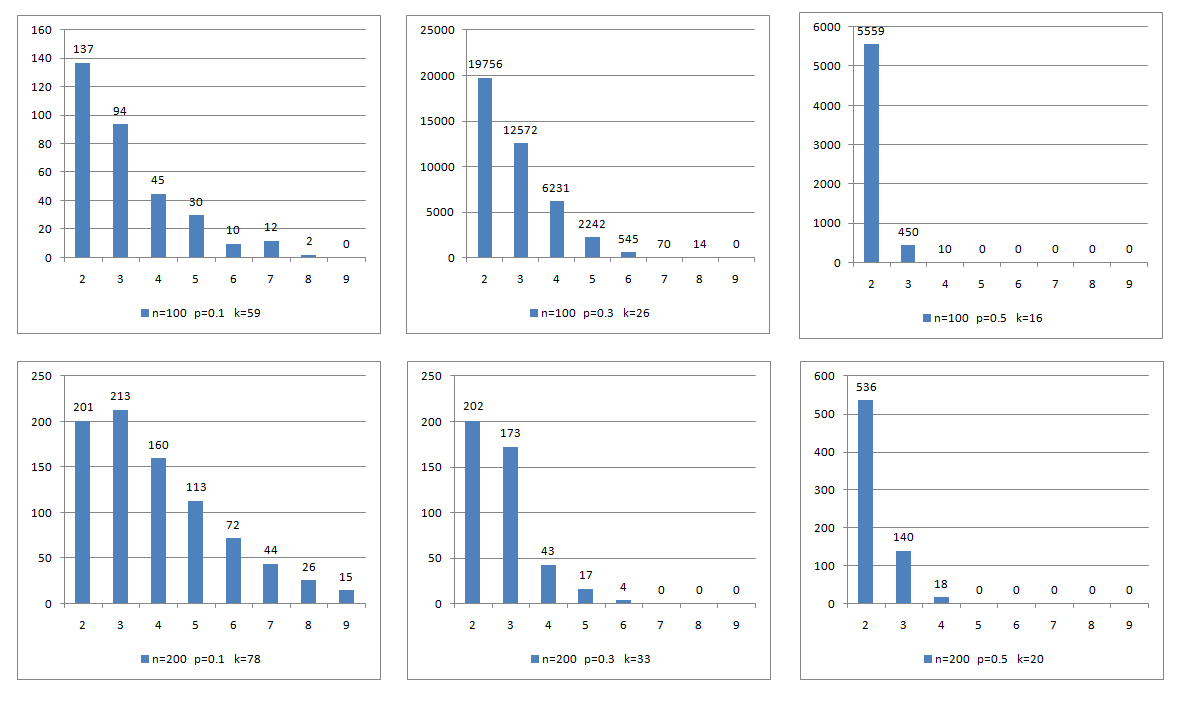
A sequence of vertices in a graph is called a legal dominating sequence if every vertex in the sequence dominates at least one vertex not dominated by those that precede it, and at the end all vertices of the graph are dominated. The Grundy domination number of a graph is the size of a largest legal dominating sequence. In this work, we introduce a generalized version of the Grundy domination problem. We explicitly calculate the corresponding parameter for paths and web graphs. We propose integer programming formulations for the new problem, find families of valid inequalities and perform extensive computational experiments to compare the formulations as well as to test these inequalities as cuts in a branch-and-cut framework. We also design and evaluate the performance of a heuristic for finding good initial lower and upper bounds and a tabu search that improves the initial lower bound. The test instances include randomly generated graphs, structured graphs, classical benchmark instances and two instances from a real application. Our approach is exact for graphs with 20-50 vertices and provides good solutions for graphs up to 10000 vertices.