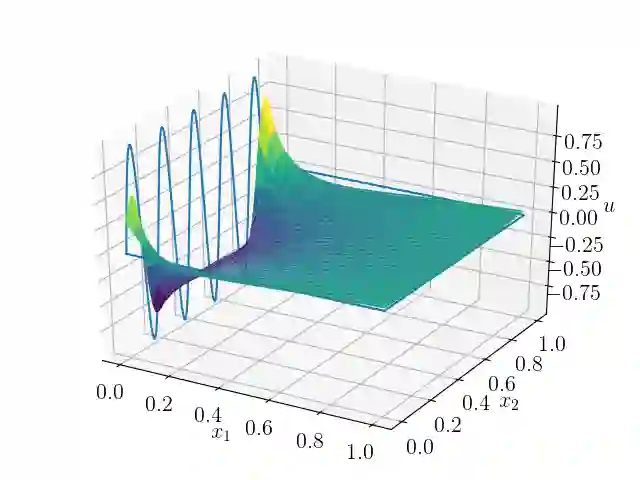
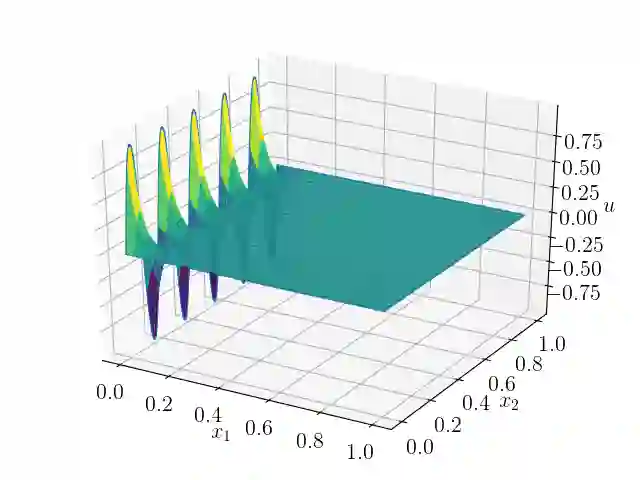
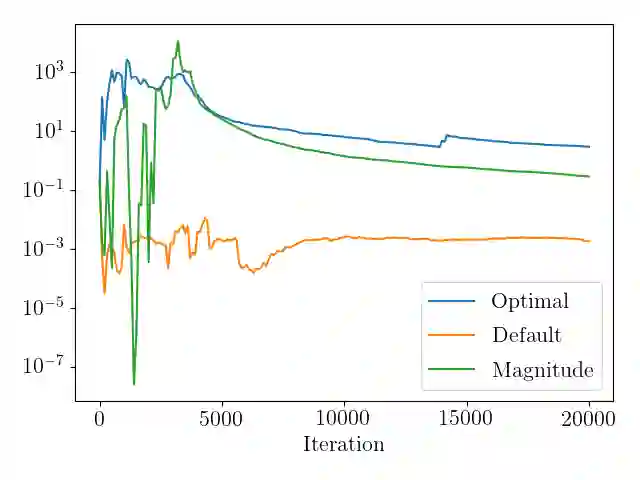
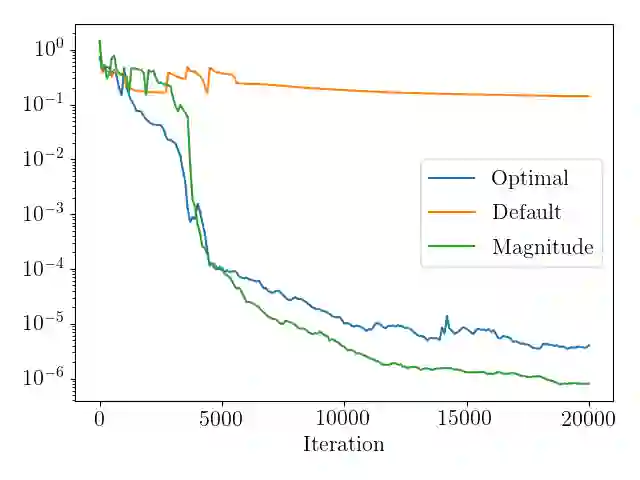
Recent works have shown that deep neural networks can be employed to solve partial differential equations, giving rise to the framework of physics informed neural networks. We introduce a generalization for these methods that manifests as a scaling parameter which balances the relative importance of the different constraints imposed by partial differential equations. A mathematical motivation of these generalized methods is provided, which shows that for linear and well-posed partial differential equations, the functional form is convex. We then derive a choice for the scaling parameter that is optimal with respect to a measure of relative error. Because this optimal choice relies on having full knowledge of analytical solutions, we also propose a heuristic method to approximate this optimal choice. The proposed methods are compared numerically to the original methods on a variety of model partial differential equations, with the number of data points being updated adaptively. For several problems, including high-dimensional PDEs the proposed methods are shown to significantly enhance accuracy.
翻译:最近的工作表明,深神经网络可以用来解决部分差异方程式,从而形成物理知情神经网络的框架。我们对这些方法采用一般化的方法,这些方法表现为一个缩放参数,平衡部分差异方程式所施加的不同限制的相对重要性。提供了这些通用方法的数学动机,表明对于线性和广泛存在的部分差异方程式来说,功能形式是共通的。然后我们为相对于相对错误的度量而言最优的缩放参数作出选择。由于这一最佳选择依赖于对分析解决方案的充分了解,我们还提议了一种粗略方法,以近似这一最佳选择。拟议方法与各种模型部分差异方程式的原始方法进行了数字比较,对数据点数进行了调整。对于一些问题,包括高维度PDEs,建议的方法显示会大大提高准确性。