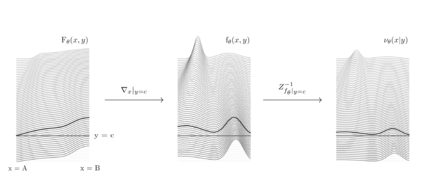
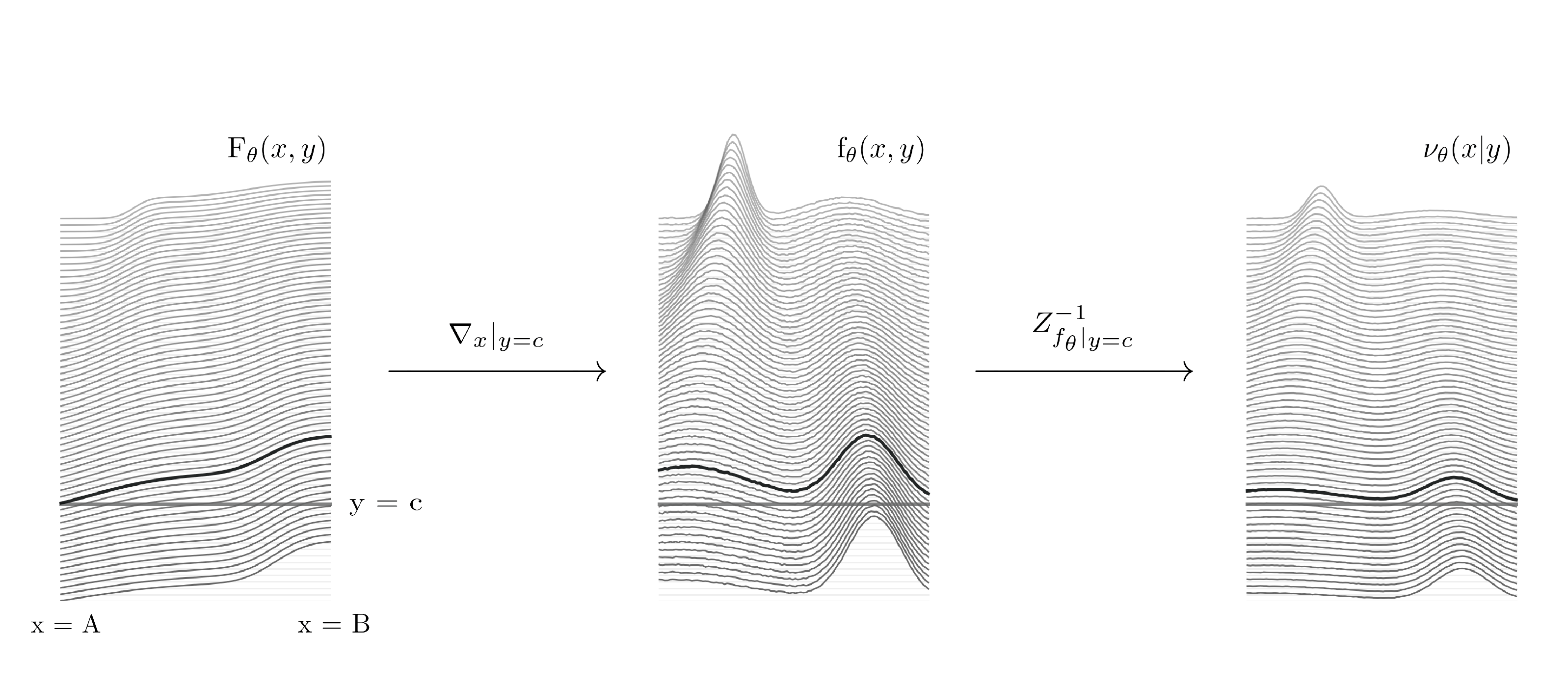
Any explicit functional representation $f$ of a density is hampered by two main obstacles when we wish to use it as a generative model: designing $f$ so that sampling is fast, and estimating $Z = \int f$ so that $Z^{-1}f$ integrates to 1. This becomes increasingly complicated as $f$ itself becomes complicated. In this paper, we show that when modeling one-dimensional conditional densities with a neural network, $Z$ can be exactly and efficiently computed by letting the network represent the cumulative distribution function of a target density, and applying a generalized fundamental theorem of calculus. We also derive a fast algorithm for sampling from the resulting representation by the inverse transform method. By extending these principles to higher dimensions, we introduce the \textbf{Neural Inverse Transform Sampler (NITS)}, a novel deep learning framework for modeling and sampling from general, multidimensional, compactly-supported probability densities. NITS is a highly expressive density estimator that boasts end-to-end differentiability, fast sampling, and exact and cheap likelihood evaluation. We demonstrate the applicability of NITS by applying it to realistic, high-dimensional density estimation tasks: likelihood-based generative modeling on the CIFAR-10 dataset, and density estimation on the UCI suite of benchmark datasets, where NITS produces compelling results rivaling or surpassing the state of the art.
翻译:当我们希望将网络用作一种基因模型时,任何明确的功能代表美元美元都受到两个主要障碍的阻碍:设计美元,以便取样速度快,并估计美元=美元=美元=美元美元,以便美元=美元=美元等于美元等于美元等于美元等于美元融合到1美元,随着美元本身变得复杂,这一点变得日益复杂。在本文中,我们表明,在用神经网络模拟单维条件密度时,如果让网络代表目标密度的累积分布功能,并应用一个普遍的基本计算公式,那么Z美元就能准确和有效地计算。我们还从由此得出的反向转变方法的表示中得出抽样的快速算法。通过将这些原则扩展至更高层面,我们引入了\ textbf{NUIFAR Inversal Inversion Transmplectr (NITS)},这是一个新的深层次学习框架,用于从一般的、多维的、靠紧凑支持的概率密度的概率密度进行建模和取样。NITS是高度直观的密度估计的密度,它以最终到最终的不同、快速抽样、精确和廉价的可能性评估。 我们通过将NITSIMFAR的高度的模型数据用于其高密度的估算。