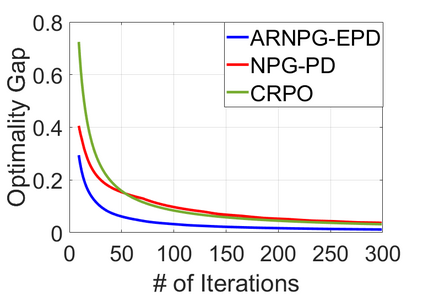
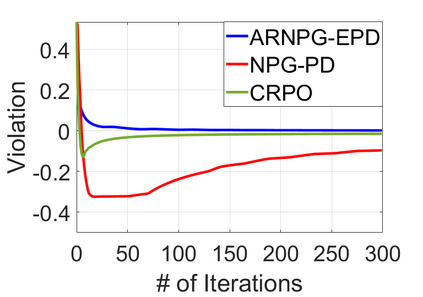
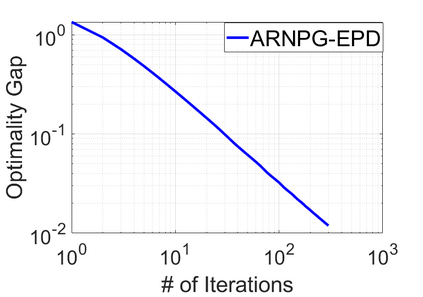
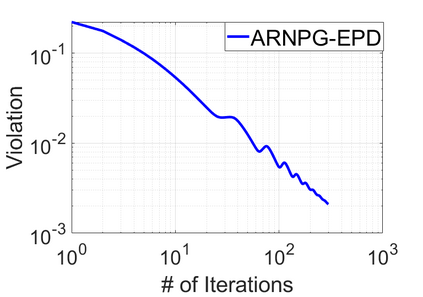
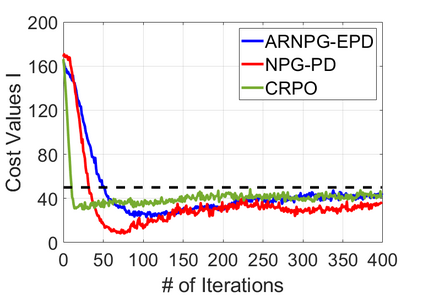
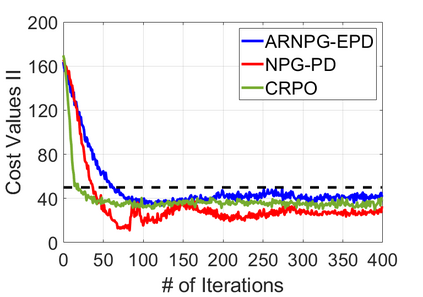
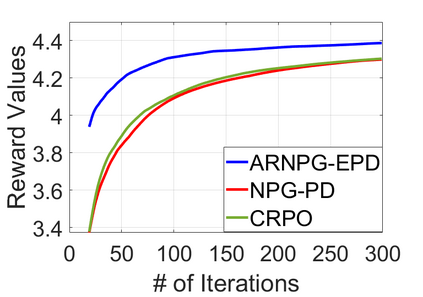
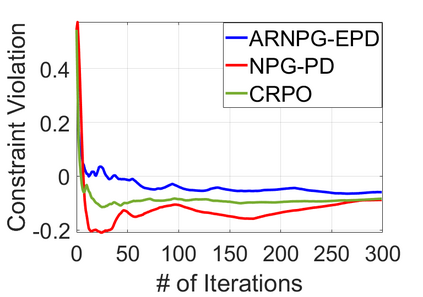
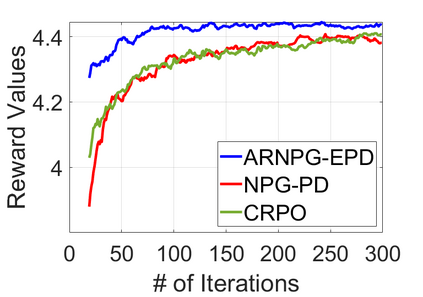
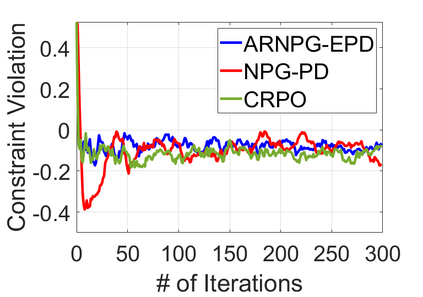
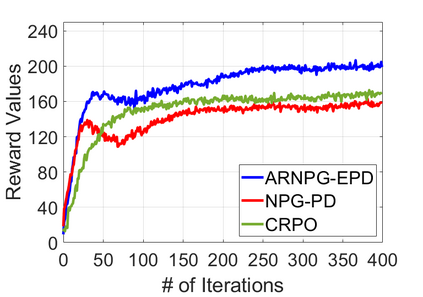
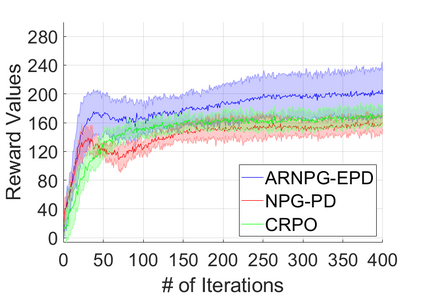
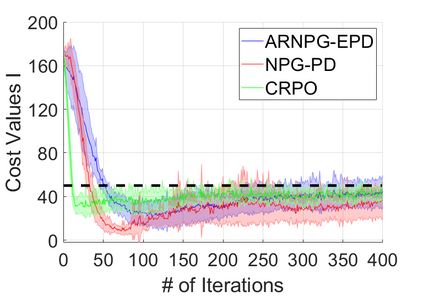
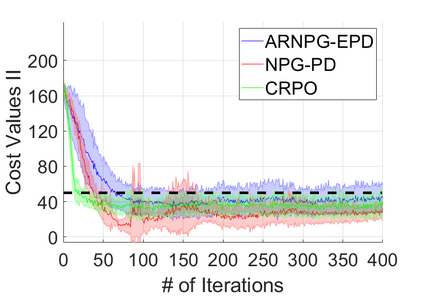
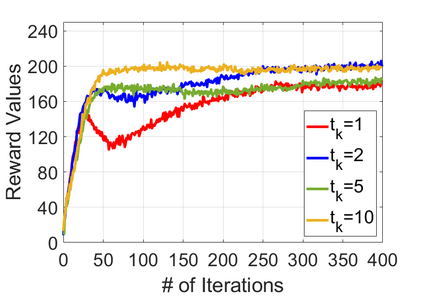
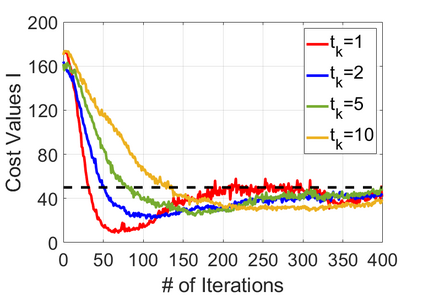
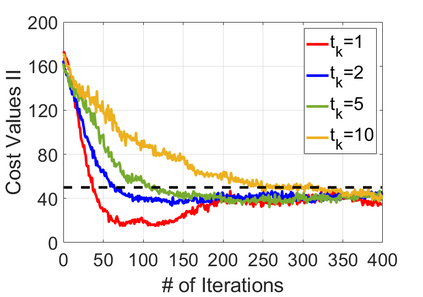
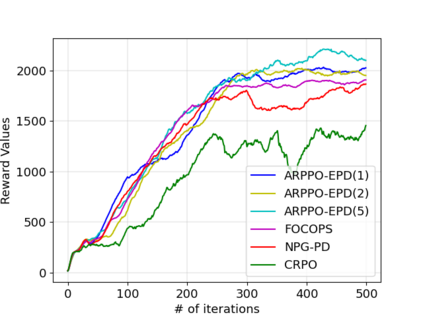
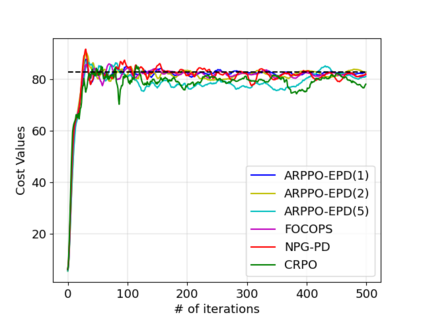
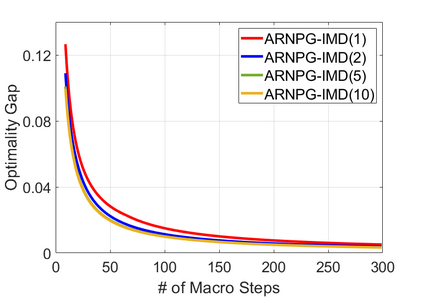
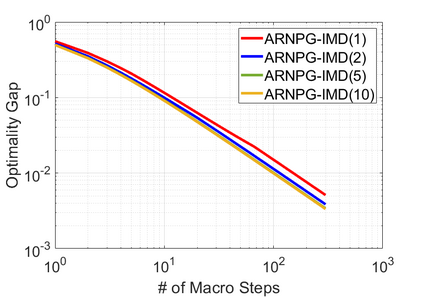
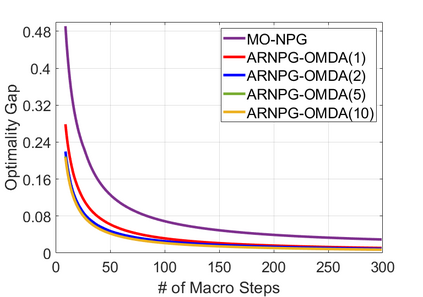
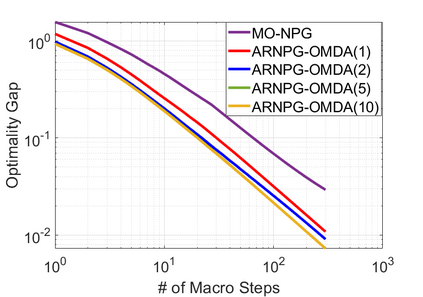
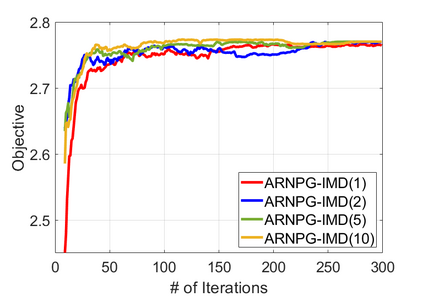
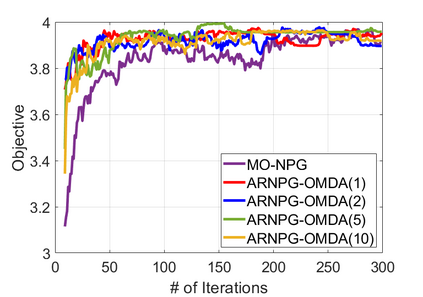
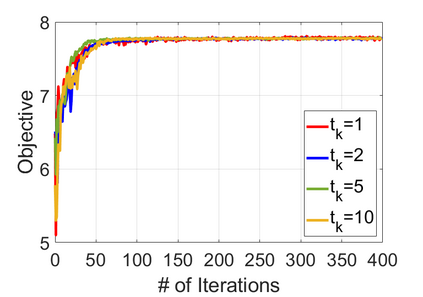
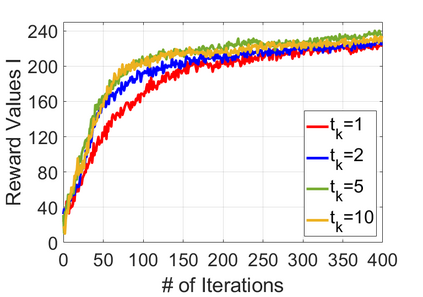
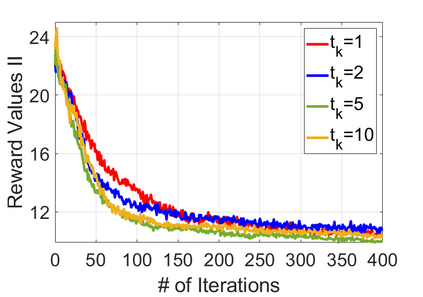
We study policy optimization for Markov decision processes (MDPs) with multiple reward value functions, which are to be jointly optimized according to given criteria such as proportional fairness (smooth concave scalarization), hard constraints (constrained MDP), and max-min trade-off. We propose an Anchor-changing Regularized Natural Policy Gradient (ARNPG) framework, which can systematically incorporate ideas from well-performing first-order methods into the design of policy optimization algorithms for multi-objective MDP problems. Theoretically, the designed algorithms based on the ARNPG framework achieve $\tilde{O}(1/T)$ global convergence with exact gradients. Empirically, the ARNPG-guided algorithms also demonstrate superior performance compared to some existing policy gradient-based approaches in both exact gradients and sample-based scenarios.
翻译:我们研究具有多种奖励价值功能的Markov决策程序的政策优化,这些功能将根据比例公平(mooth concave scalalization)、硬性制约(contraced MDP)和最大幅度权衡等特定标准共同优化。 我们提议了一个“固定调整自然政策梯度(ARNPG)框架 ”, 该框架可以在设计多目标 MDP问题的政策优化算法时系统地纳入业绩良好的一级方法。理论上,基于ARNPG 框架的设计算法实现了与精确梯度的全球趋同 $\ tilde{O}(1/T) 。 简而言之,ARNPG 指导算法在精确的梯度和基于样本的情景中也表现出优于某些现行基于梯度的政策方法的绩效。