Diffusion Means in Geometric Spaces

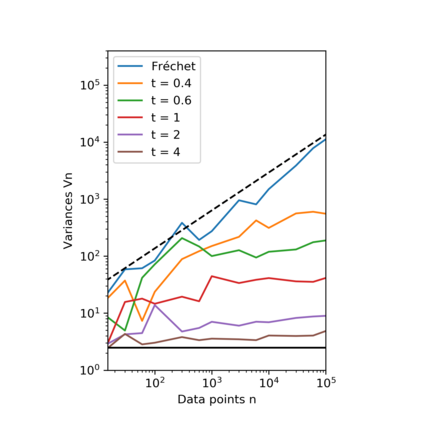
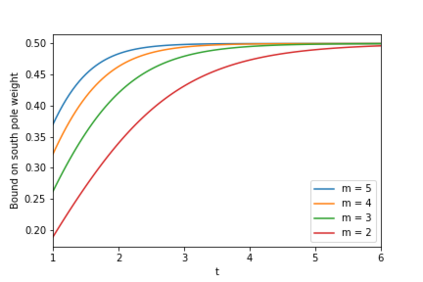
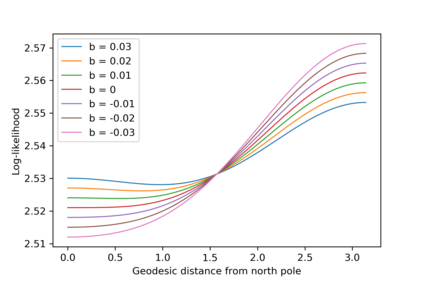
We introduce a location statistic for distributions on non-linear geometric spaces, the diffusion mean, serving both as an extension of and an alternative to the Fr\'echet mean. The diffusion mean arises as the generalization of Gaussian maximum likelihood analysis to non-linear spaces by maximizing the likelihood of a Brownian motion. The diffusion mean depends on a time parameter $t$, which admits the interpretation of the allowed variance of the mean. The diffusion $t$-mean of a distribution $X$ is the most likely origin of a Brownian motion at time $t$, given the end-point distribution $X$. We give a detailed description of the asymptotic behavior of the diffusion estimator and provide sufficient conditions for the diffusion estimator to be strongly consistent. Furthermore, we present a smeary central limit theorem for diffusion means and investigate properties of the diffusion mean for distributions on the sphere $\mathcal{S}^n$. Experimentally, we consider simulated data and data from magnetic pole reversals, all indicating similar or improved convergence rate compared to the Fr\'echet mean. Here, we additionally estimate $t$ and consider its effects on smeariness and uniqueness of the diffusion mean for distributions on the sphere.