Divergence-Free Flux Globalization Based Well-Balanced Path-Conservative Central-Upwind Schemes for Rotating Shallow Water Magnetohydrodynamics

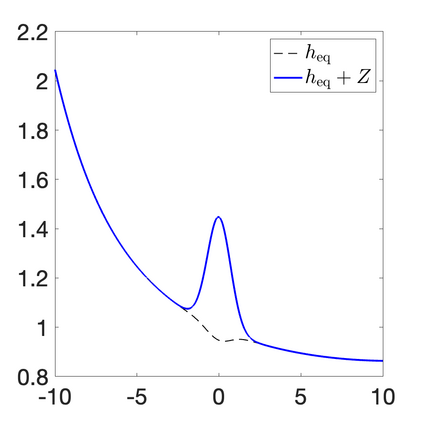
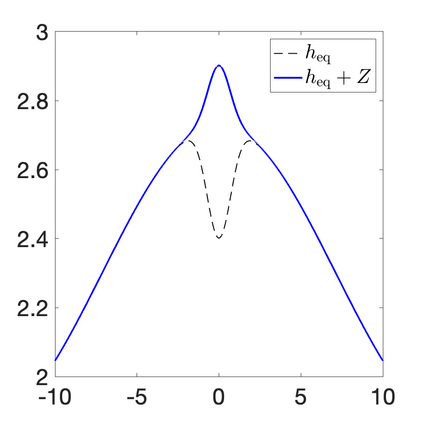
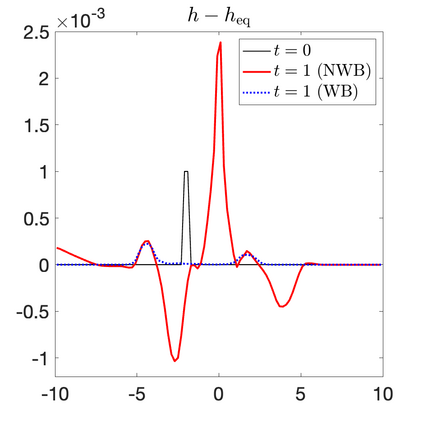
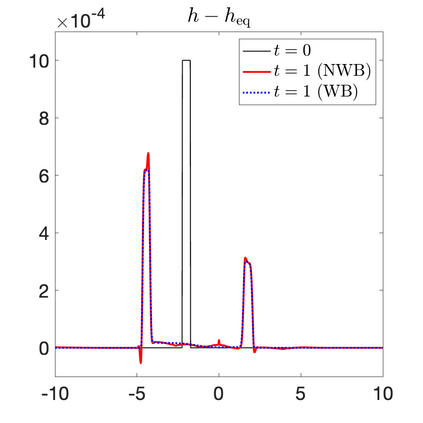
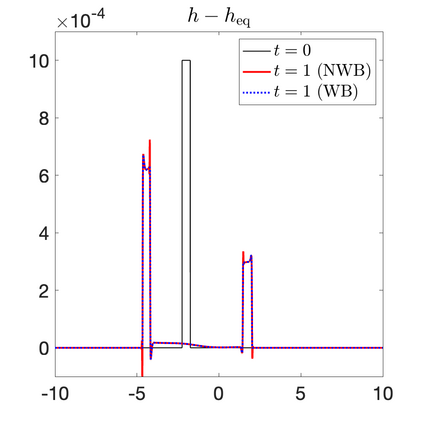
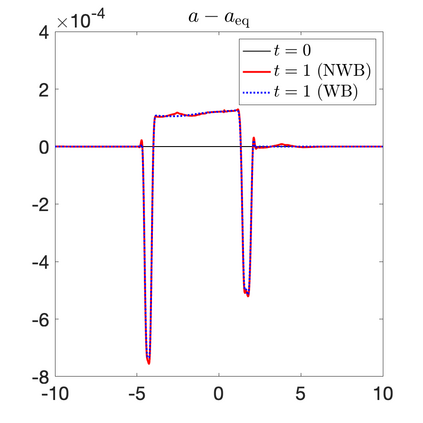
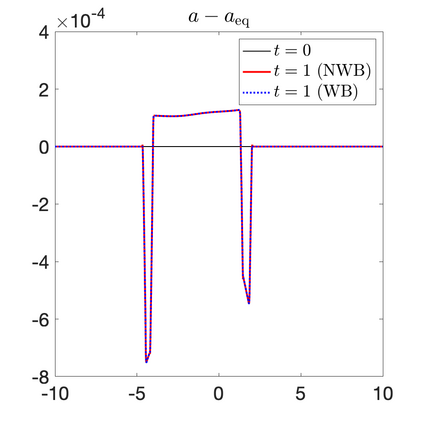
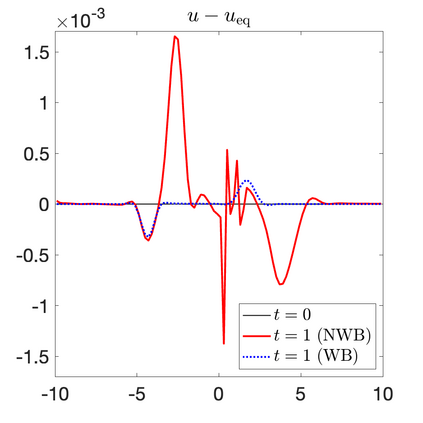
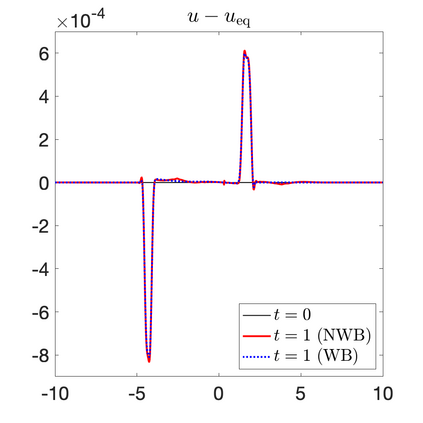
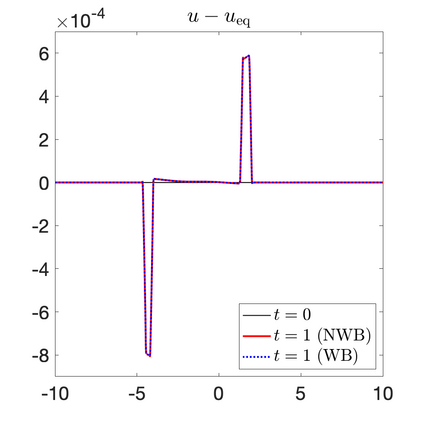
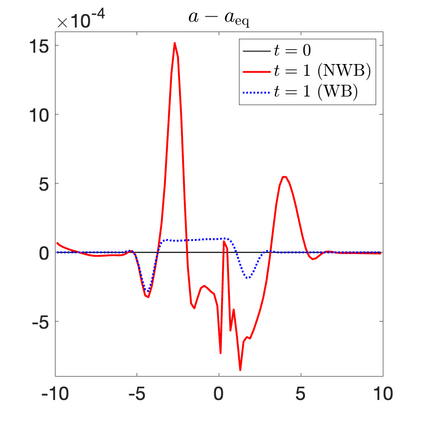
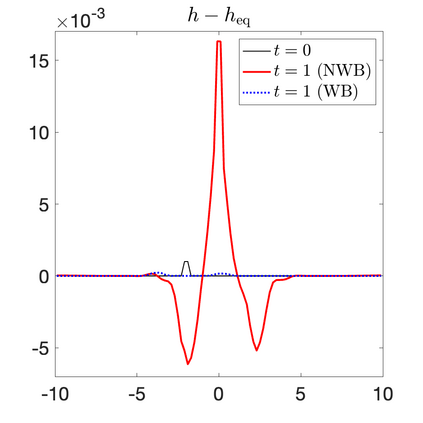
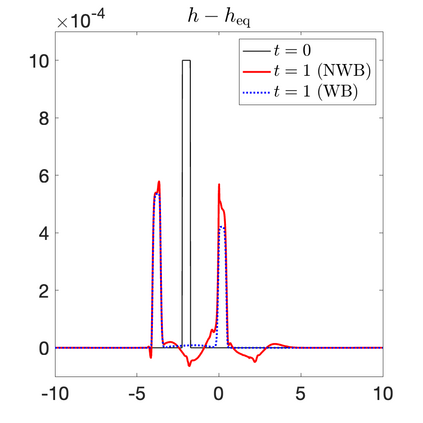
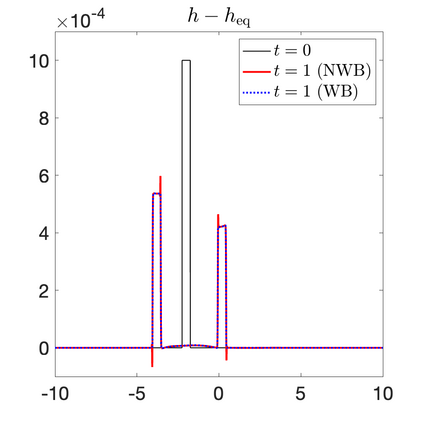
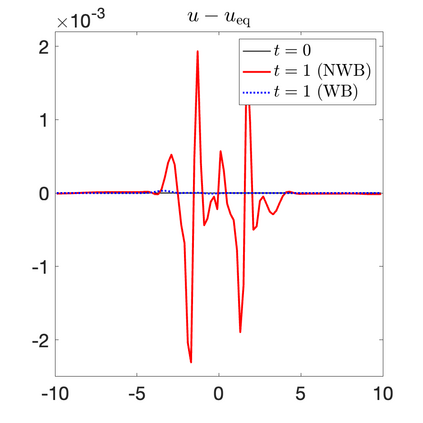
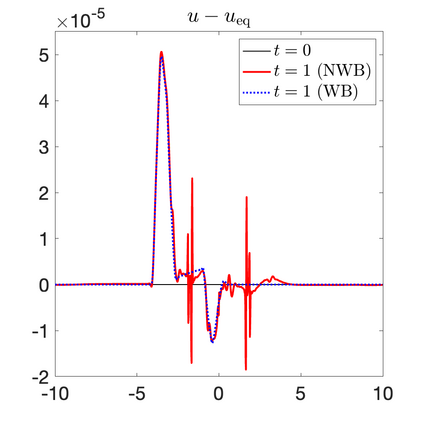
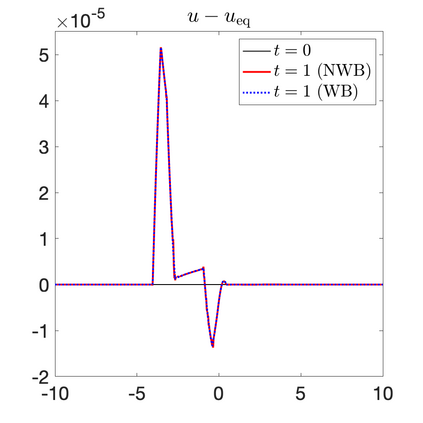
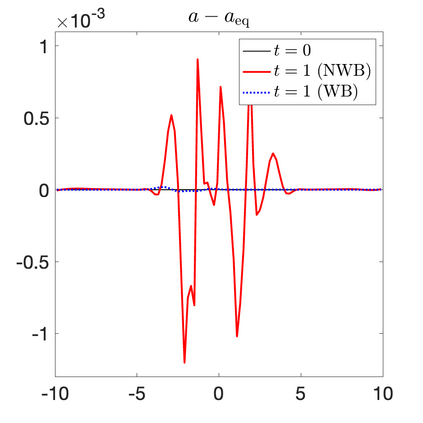
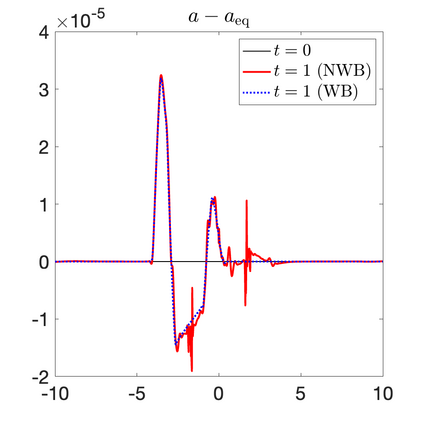
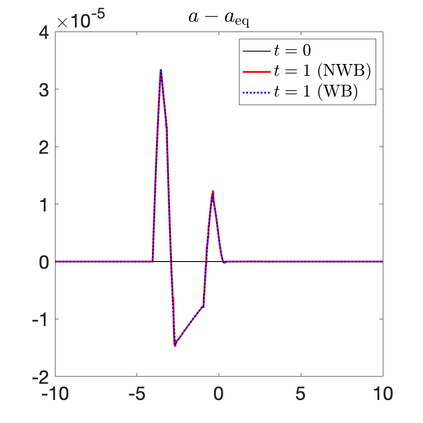
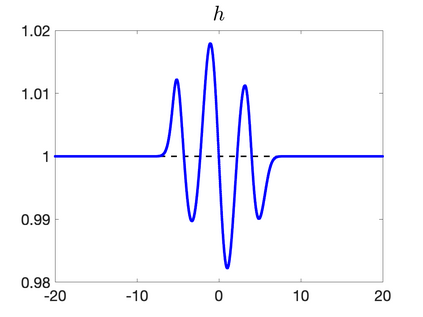
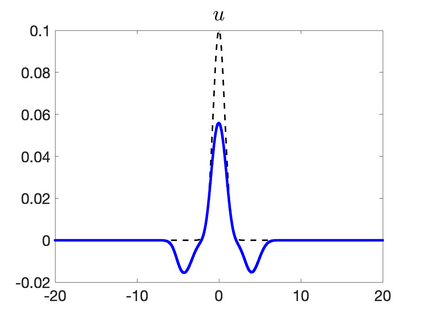
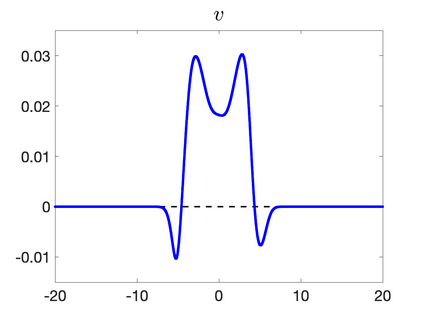
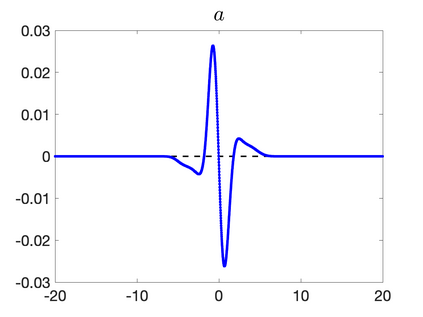
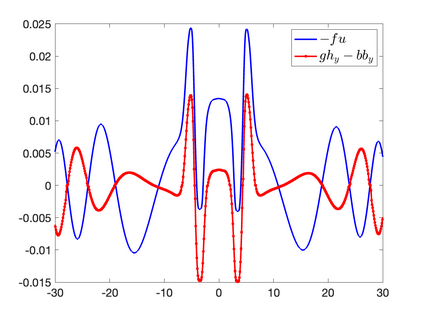
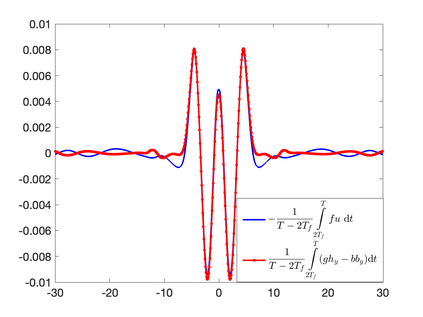
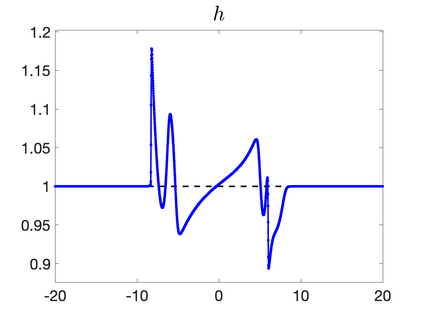
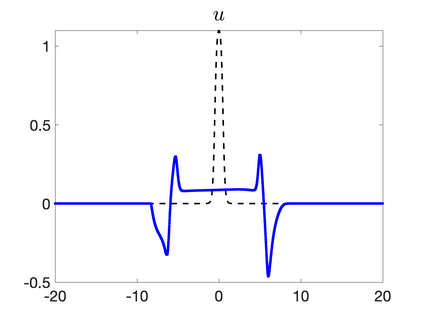
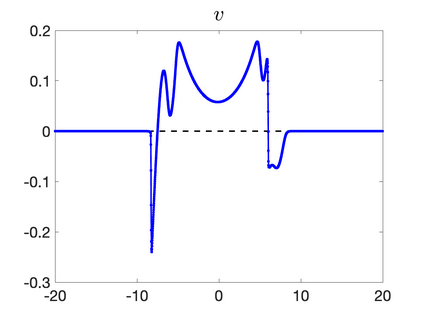
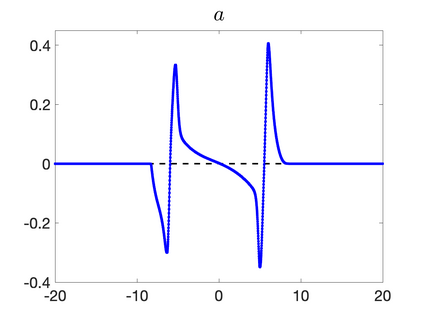
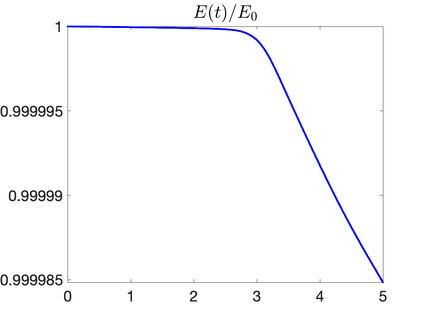
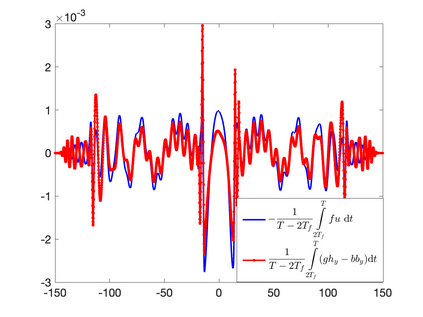
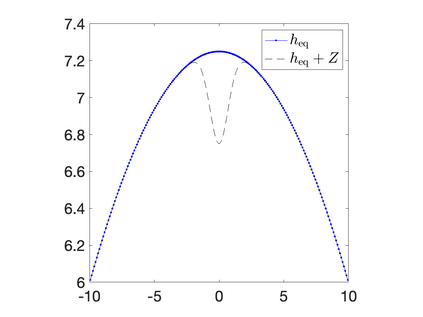
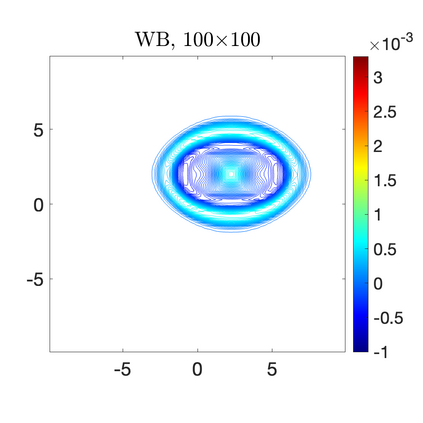
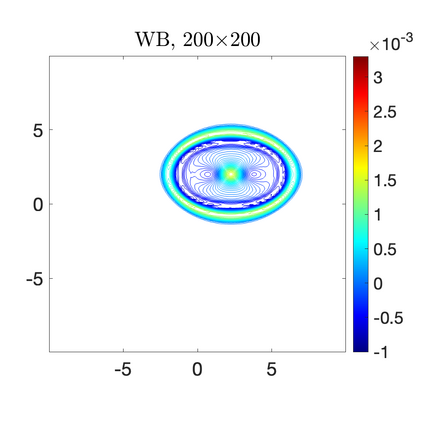
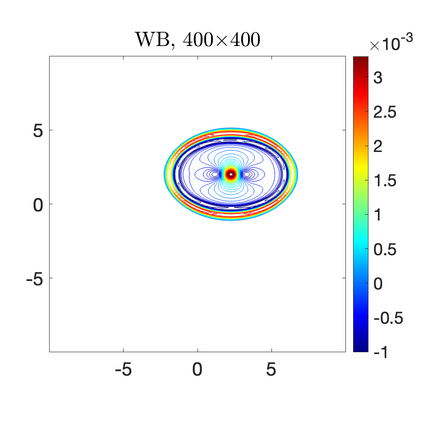
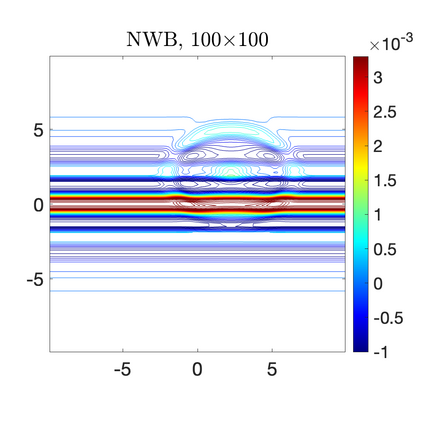
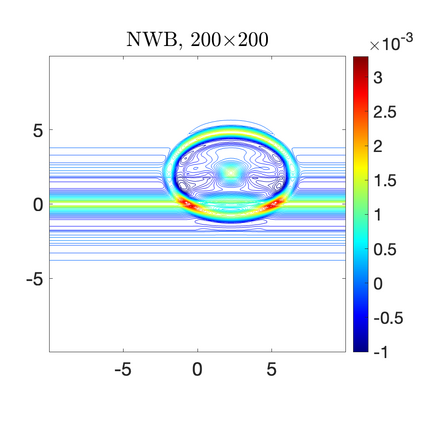
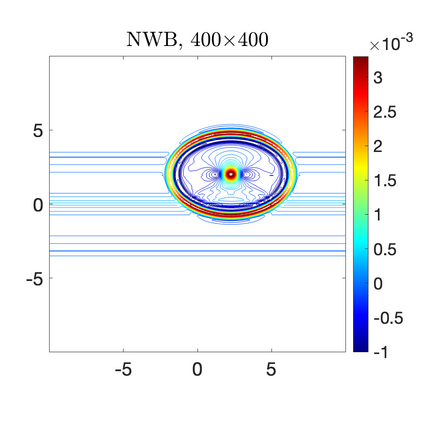
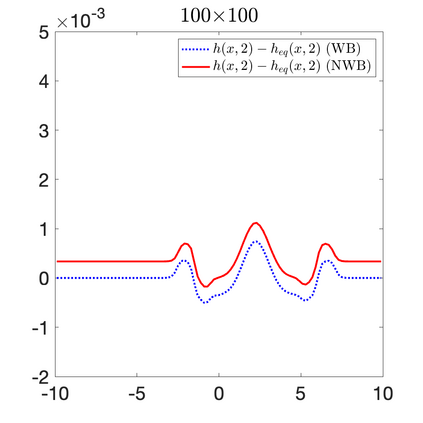
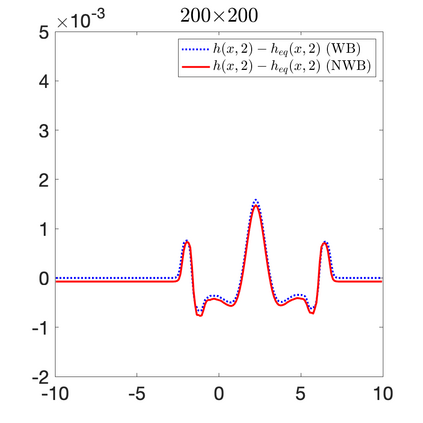
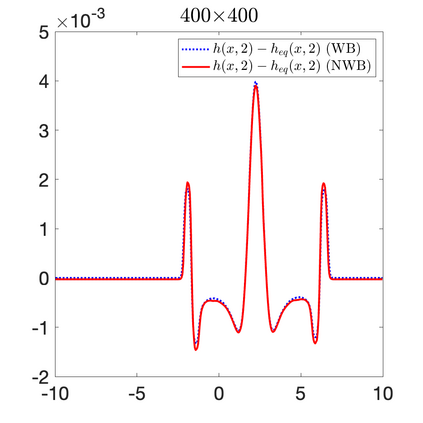
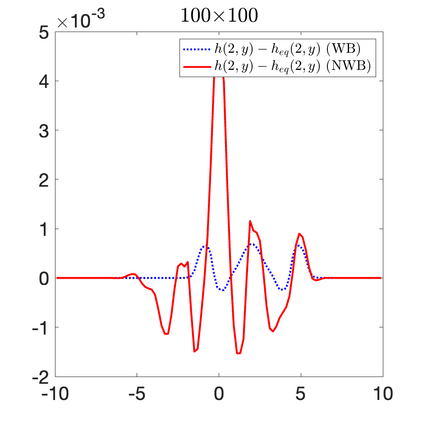
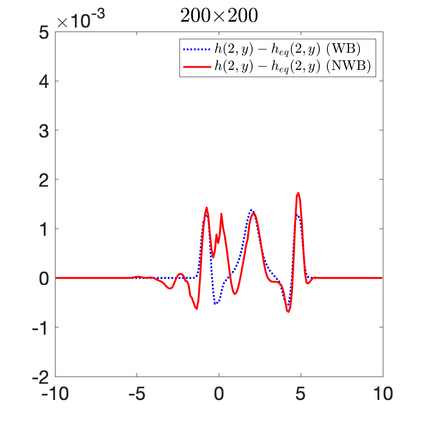
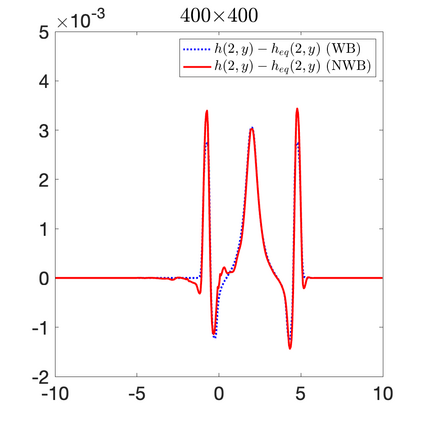
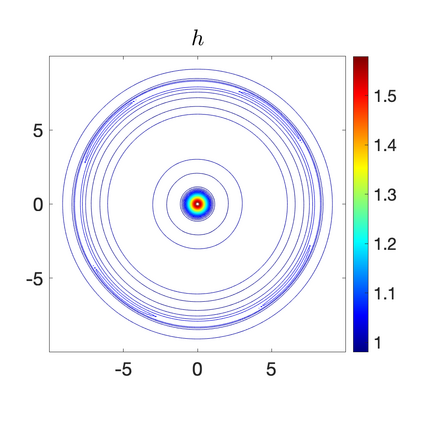
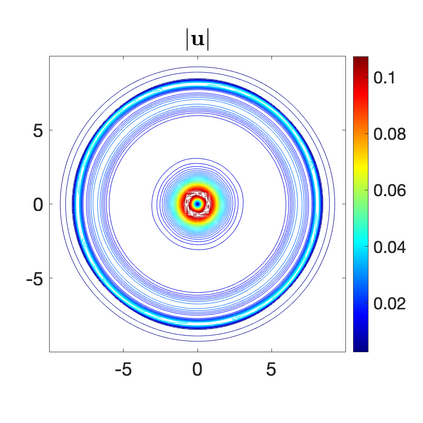
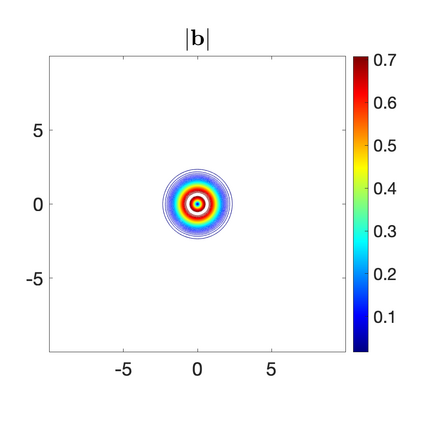
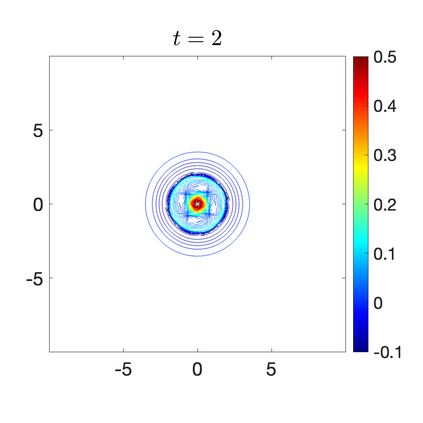
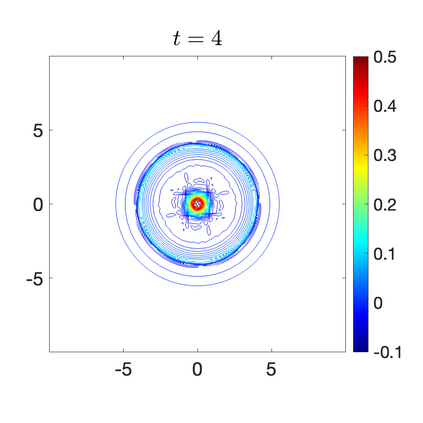
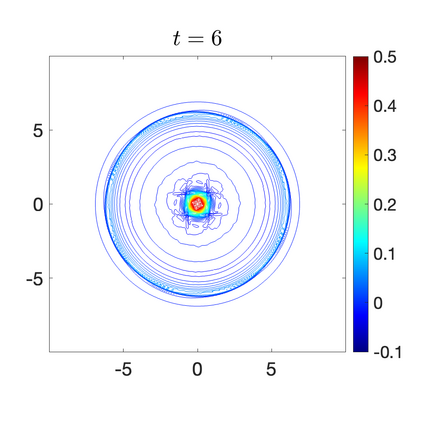
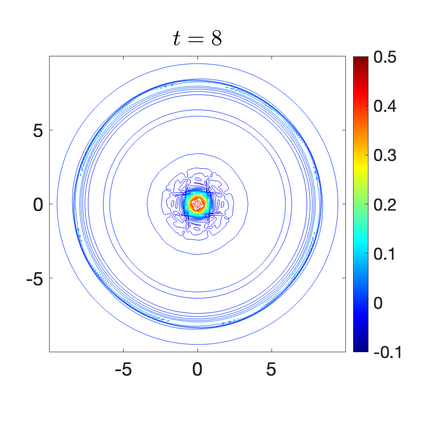
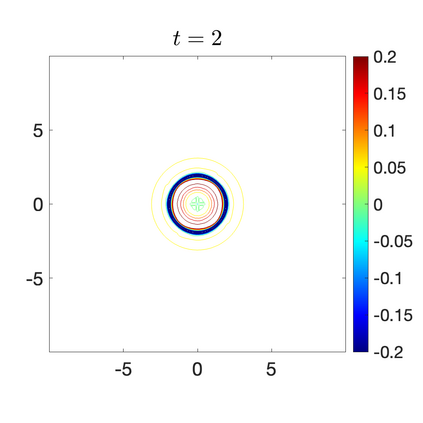
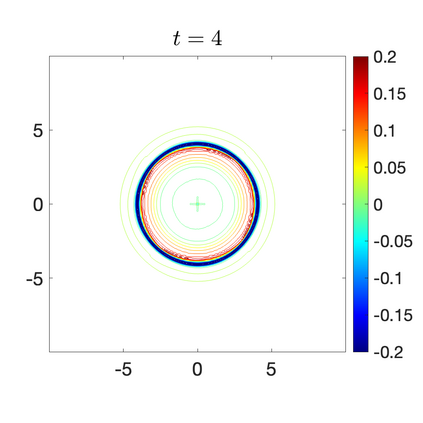
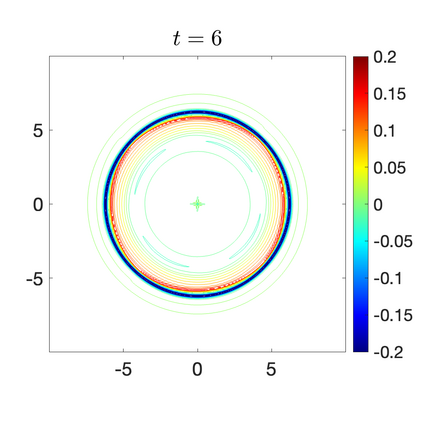
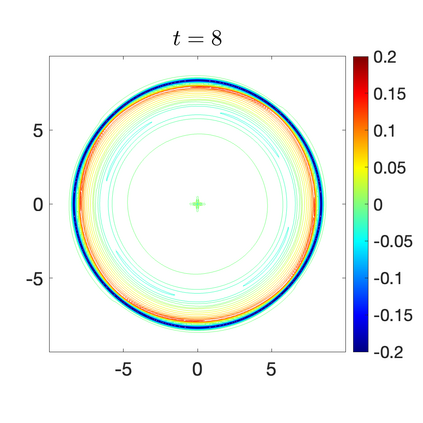
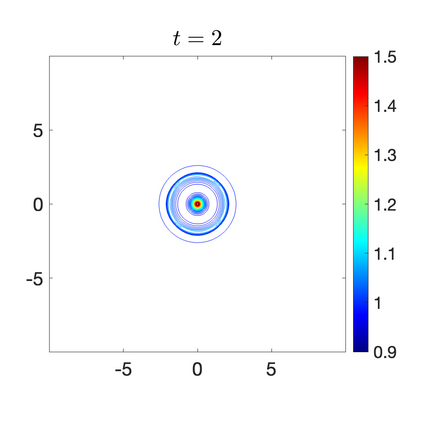
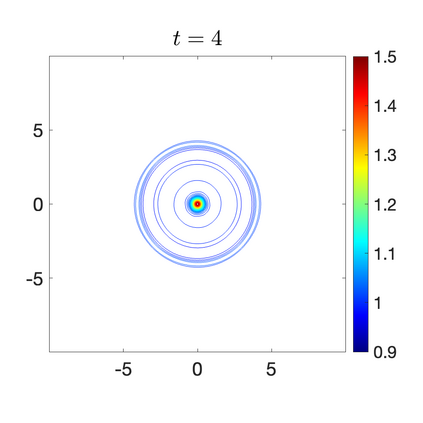
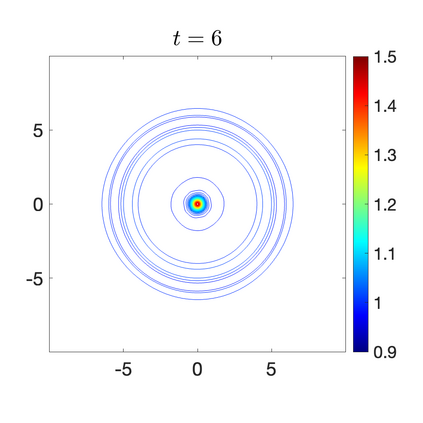
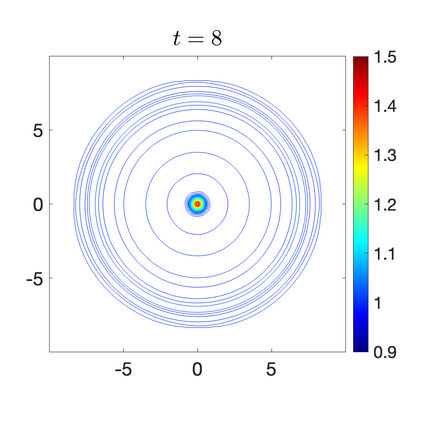
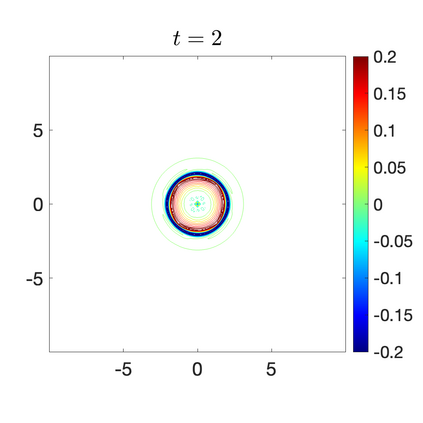
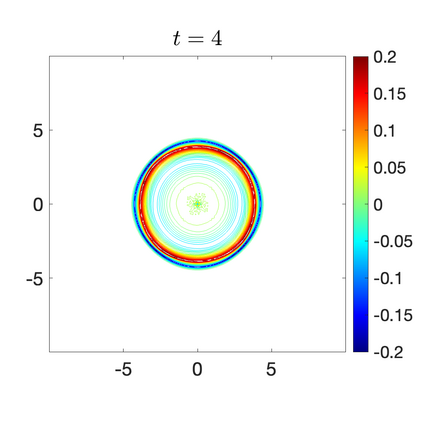
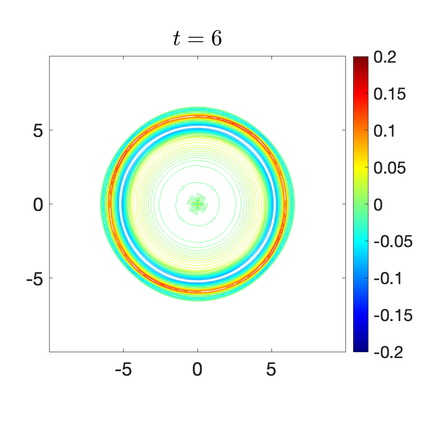
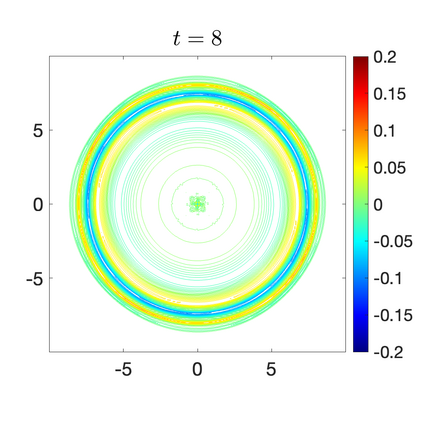
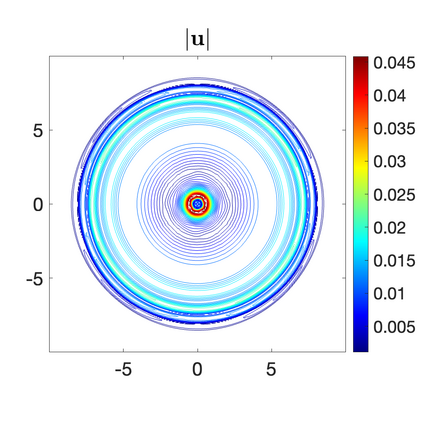
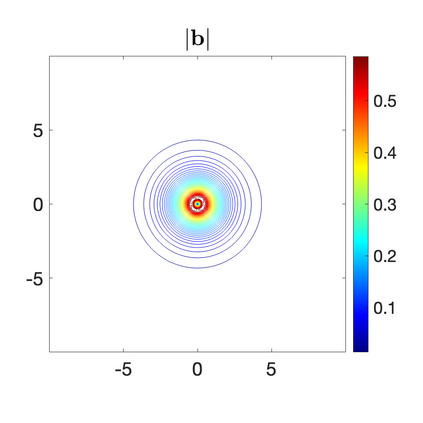
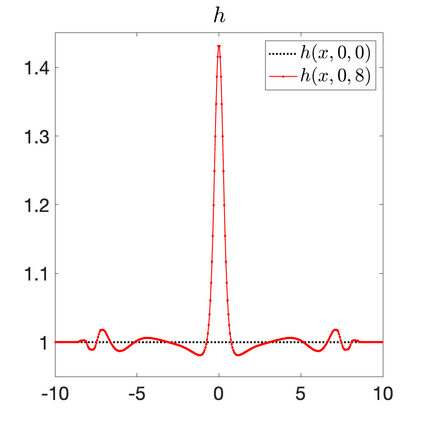
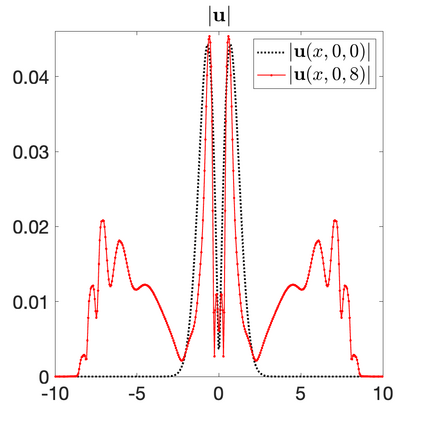
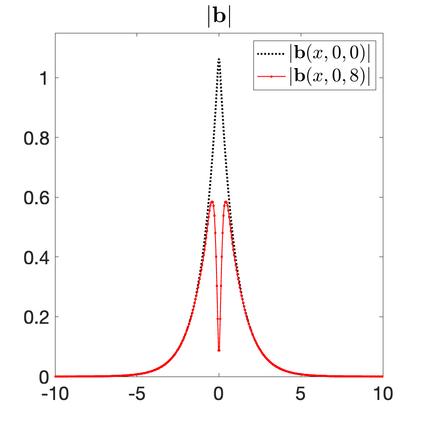
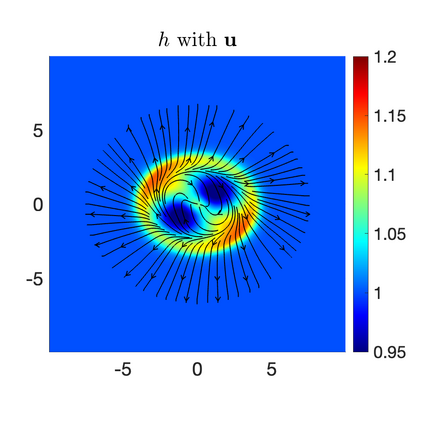
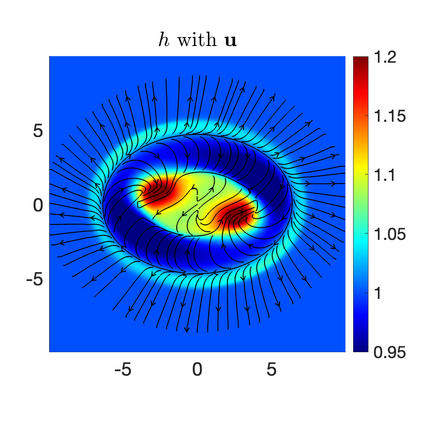
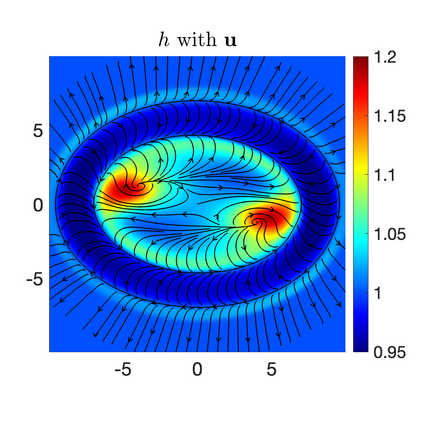
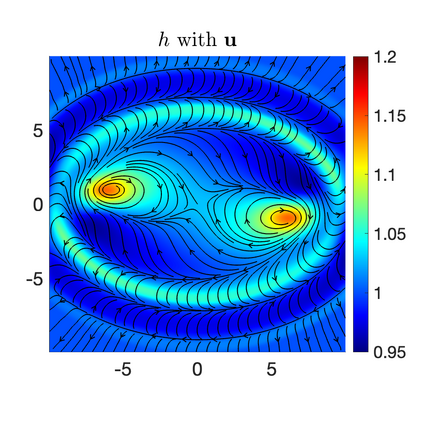
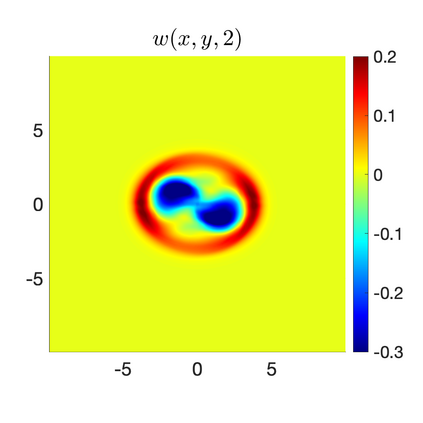
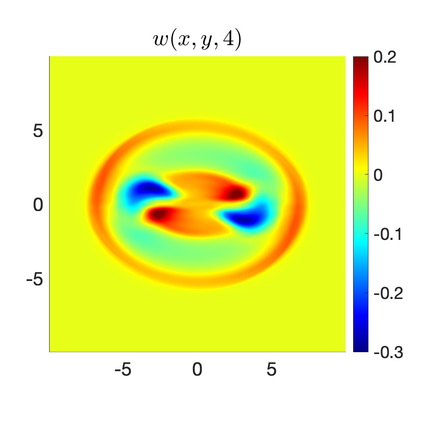
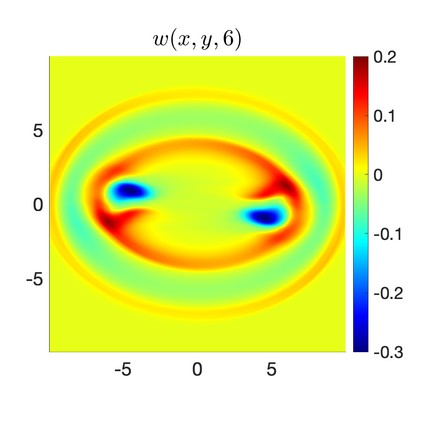
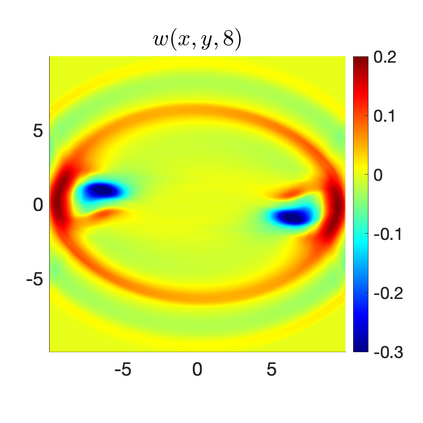
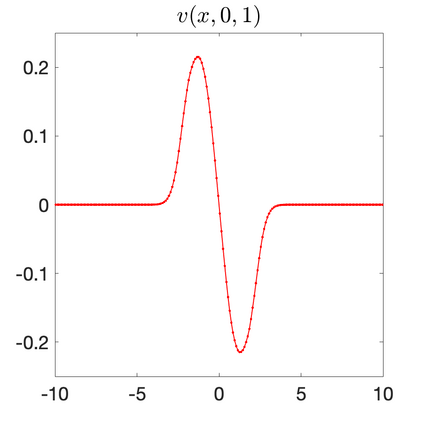
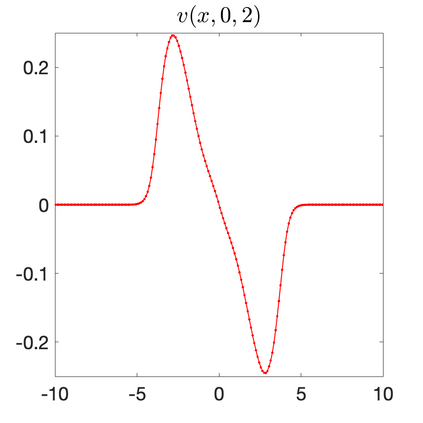
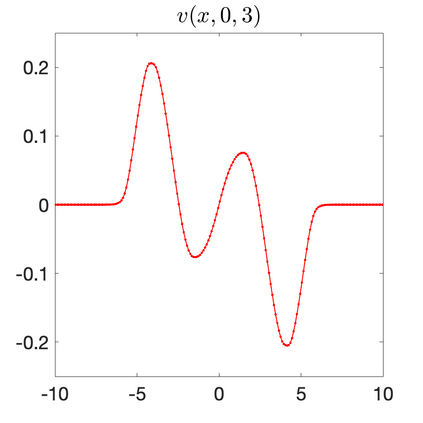
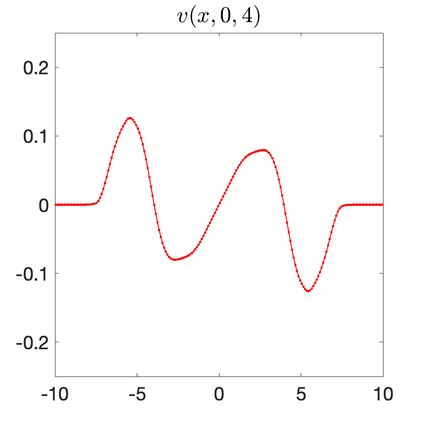
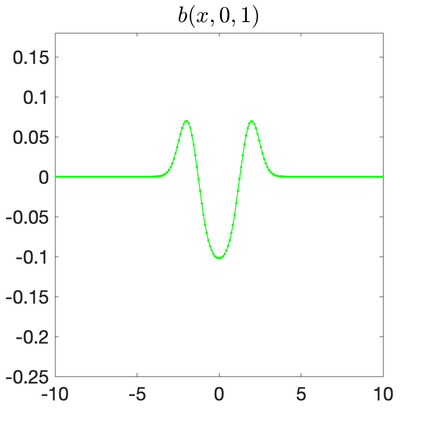
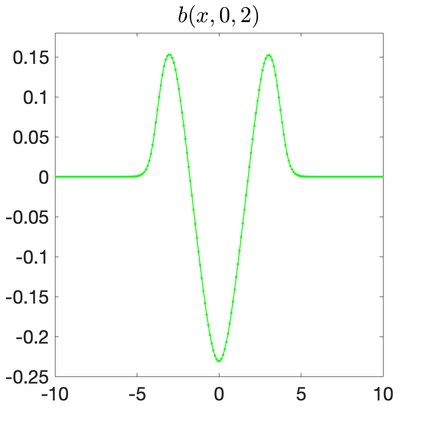
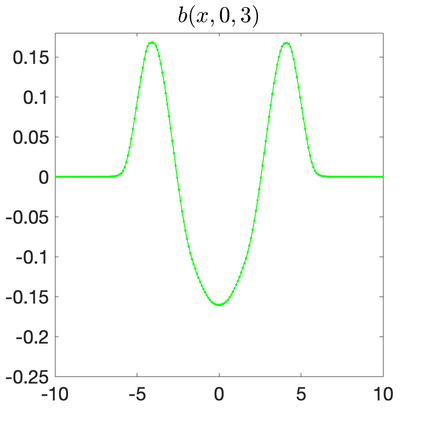
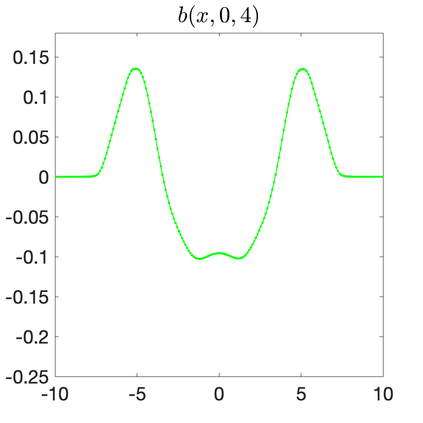
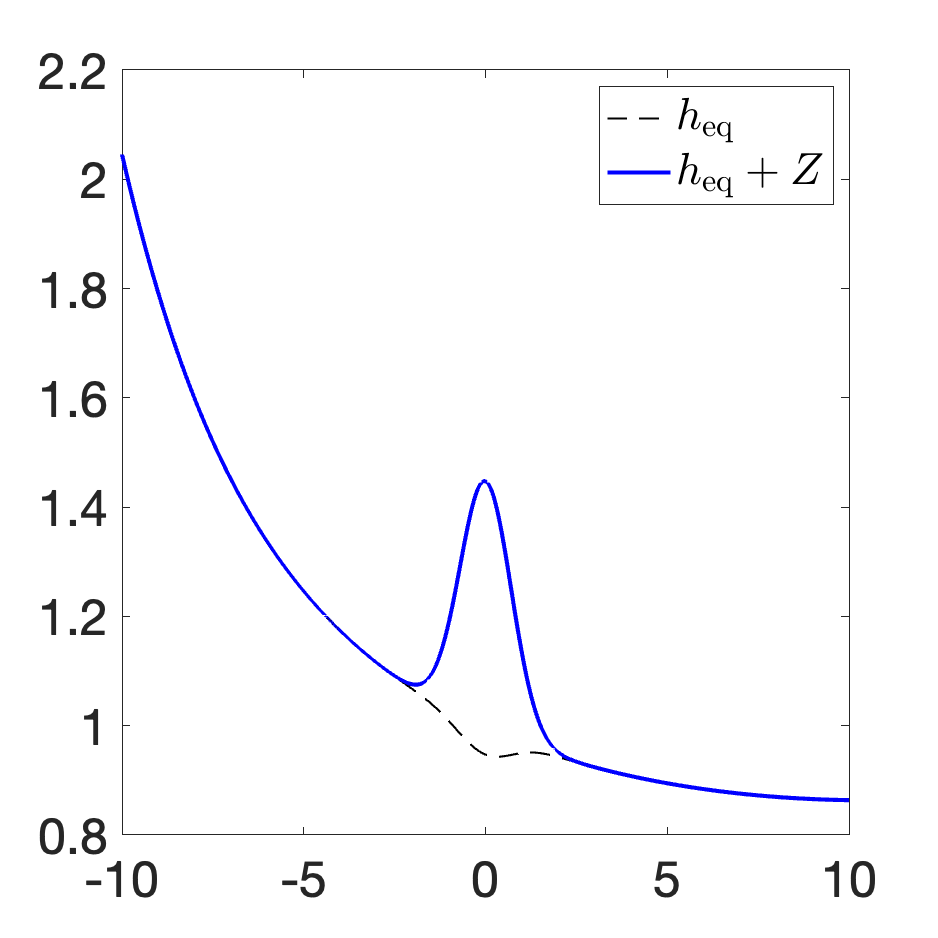
We develop a new second-order flux globalization based path-conservative central-upwind (PCCU) scheme for rotating shallow water magnetohydrodynamic equations. The new scheme is designed not only to maintain the divergence-free constraint of the magnetic field at the discrete level but also to satisfy the well-balanced (WB) property by exactly preserving some physically relevant steady states of the underlying system. The locally divergence-free constraint of the magnetic field is enforced by following the method recently introduced in [A. Chertock, A. Kurganov, M. Redle, and K. Wu, ArXiv preprint (2022), arXiv:2212.02682]: we consider a Godunov-Powell modified version of the studied system, introduce additional equations by spatially differentiating the magnetic field equations, and modify the reconstruction procedures for magnetic field variables. The WB property is ensured by implementing a flux globalization approach within the PCCU scheme, leading to a method capable of preserving both still- and moving-water equilibria exactly. In addition to provably achieving both the WB and divergence-free properties, the new method is implemented on an unstaggered grid and does not require any (approximate) Riemann problem solvers. The performance of the proposed method is demonstrated in several numerical experiments that confirm the lack of spurious oscillations, robustness, and high resolution of the obtained results.