A tiny public key scheme based on Niederreiter Cryptosystem

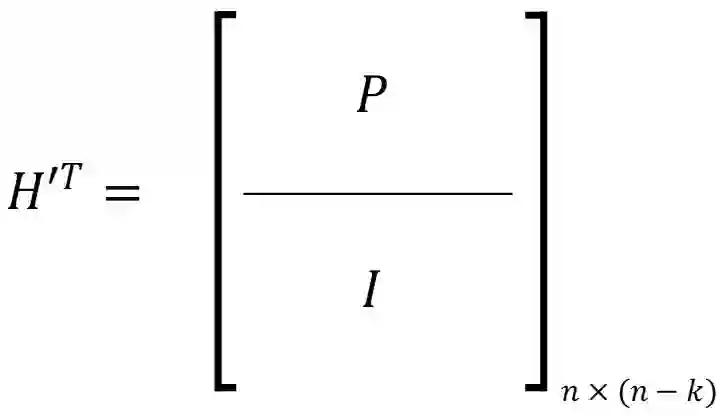
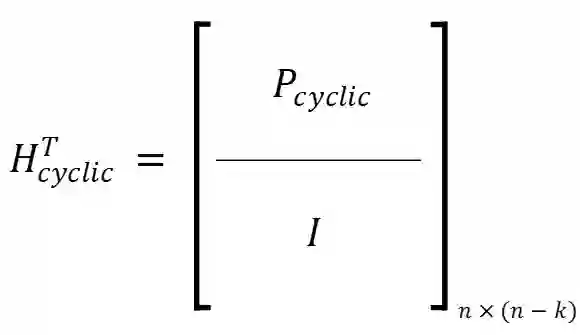
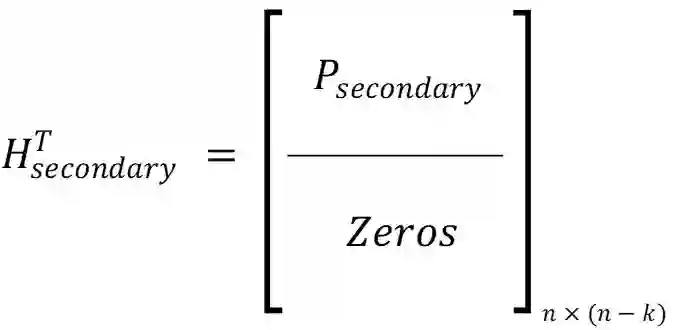
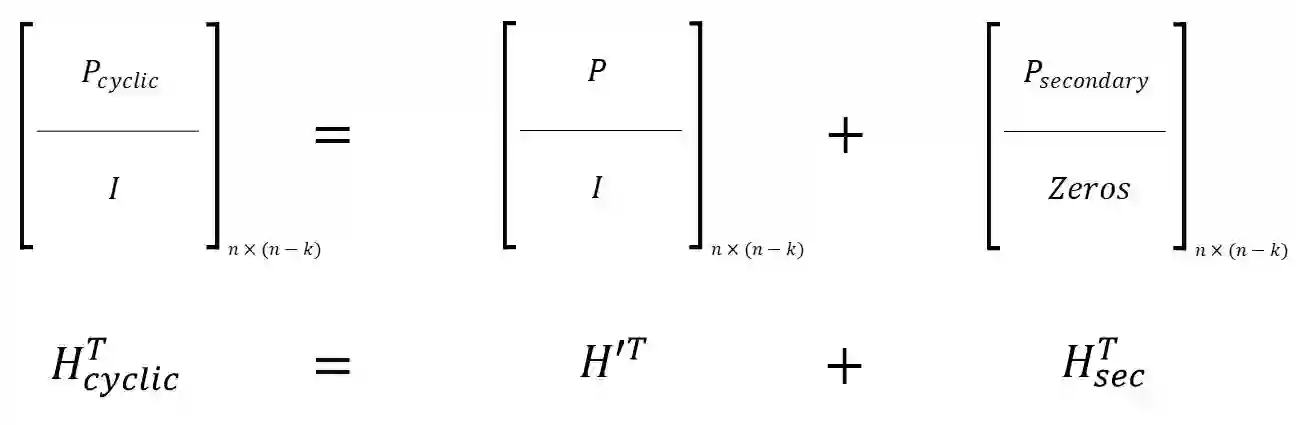
Due to the weakness of public key cryptosystems encounter of quantum computers, the need to provide a solution was emerged. The McEliece cryptosystem and its security equivalent, the Niederreiter cryptosystem, which are based on Goppa codes, are one of the solutions, but they are not practical due to their long key length. Several prior attempts to decrease the length of the public key in code-based cryptosystems involved substituting the Goppa code family with other code families. However, these efforts ultimately proved to be insecure. In 2016, the National Institute of Standards and Technology (NIST) called for proposals from around the world to standardize post-quantum cryptography (PQC) schemes to solve this issue. After receiving of various proposals in this field, the Classic McEliece cryptosystem, as well as the Hamming Quasi-Cyclic (HQC) and Bit Flipping Key Encapsulation (BIKE), chosen as code-based encryption category cryptosystems that successfully progressed to the final stage. This article proposes a method for developing a code-based public key cryptography scheme that is both simple and implementable. The proposed scheme has a much shorter public key length compared to the NIST finalist cryptosystems. The key length for the primary parameters of the McEliece cryptosystem (n=1024, k=524, t=50) ranges from 18 to 500 bits. The security of this system is at least as strong as the security of the Niederreiter cryptosystem. The proposed structure is based on the Niederreiter cryptosystem which exhibits a set of highly advantageous properties that make it a suitable candidate for implementation in all extant systems.