Quantification and aggregation over concepts of the ontology

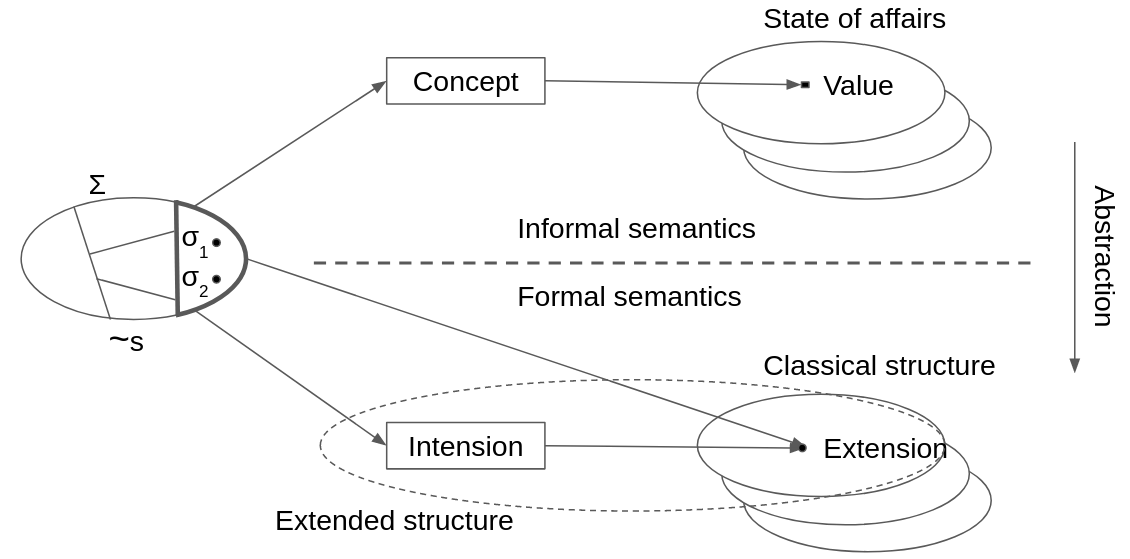
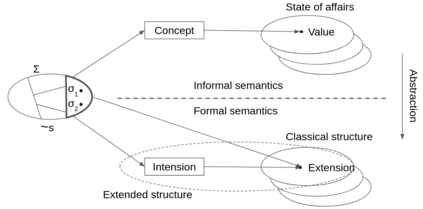
This paper focuses on quantifications whose nature, we believe, is generally undervalued within the Knowledge Representation community: they range over a set of concepts, i.e., of intensional objects identified in the ontology. Hence, we extend first order logic to allow referring to the intension of a symbol, i.e., to the concept it represents. Our formalism is more elaboration tolerant than simpler formalisms that require reification, but also introduces the possibility of syntactically incorrect formula.We introduce a guarding mechanism to make formula syntactically correct, and present a method to verify correctness. The complexity of the method is linear with the length of the formula. We also extend FO($\cdot$) (aka FO-dot), a logic-based knowledge representation language, in a similar way, and show how it helped solve practical problems. The value of expressing intensional statements has been well-established in modal logic. We show how our approach expands on the understanding of intensions as studied in modal settings by, e.g., Fitting, in a way that is of value in non-modal settings as well.